Complex number在ALEVEL高数的学习中存在感非常高，最可怕的就是复数图像还喜欢和几何问题凑在一起出题，很多同学一碰到这类题就凉凉。今天就为大家介绍3类ALEVEL高数复数图像，读懂图就离答对题不远啦。
1
复数平面
复数平面即是z=a+bi ,和大家熟悉的x-y轴有点像。它对应的坐标为（a,b) .其中，a表示的是复平面内的横坐标，b表示的是复平面内的纵坐标，表示实数a的点都在x轴上，所以x轴又称为“实轴”；表示纯虚数bi的点都在y轴上，所以y轴又称为“虚轴”。y轴上有且仅有一个实点即为原点"0"。
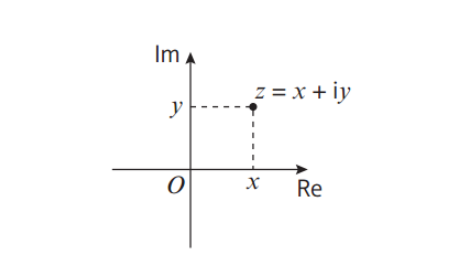
2
复数的模和角
在复数中，一个很重要的概念是复数的模（Modulus）和角（Argument），也即是复数对应的点，到平面原点的距离r，和到平面原点连线和实数轴正半轴的夹角θ。三个最重要的复数图形，也都是由r和θ来表示的。
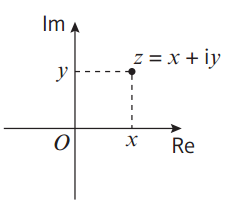
01圆的图像
表达式：|z - z1| = r 或是 |z - (x1+ iy1)| = r
解释：z - z1 或是z - (x1+ iy1)意为z到另外一点z1 (x1,y1) 的连线，加了绝对值符号意为距离为r，也就是说，z位于一个圆心是z1 (x1,y1)，半径为r的圆上。
02垂直平分线
表达式：|z − z1| = |z − z2|
解释：z1和z2是阿甘特图中的另外两个点，表达式意为z到这两个点的距离相等，那么满足条件的所有的点，就一定在z1和z2两点连线的垂直平分线上。
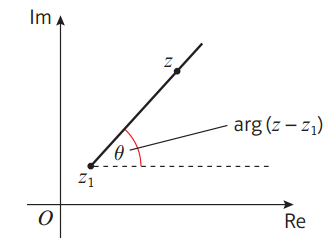
3、射线
表达式：arg (z − z1) = θ
解释：arg符号代表角的意思，z- z1代表z和另外一点的连线，也就是两点连线成某一个角度，是一条以z1为出发点，和水平方向成θ角的射线。
有关ALEVEL高数3类复数图像的介绍就到这里，希望能帮助你对这些图像有更本质的了解。
如果你是爱德思考试局的学员，那么现在就可以开始为1月大考做准备啦。参加一月大考不仅可以使得我们节省下更多时间为后续申请做准备，也许还能让你多考一门成绩。如果想利用剩下2个月的时间高效复习，点击报名【ALEVEL同步培训班】，集中梳理考试重难点，弥补知识漏洞，高强度输出考试技巧。
更多ALEVEL学习攻略点击ALEVEL数学D1怎么复习？考点与易错点都帮你整理好啦、
ALEVEL生物A2光合作用、有氧呼吸作用精讲，白送分还不要吗？
快扫码
关注老师微信
潘田翰(创始人)
剑桥大学化学工程硕士
Candise Cai
牛津大学化学硕士
Chris Chen
帝国理工学院物理学士
Ruby Rui
剑桥大学经济系学士&双硕士学位
Elaine Xu
牛津大学数学与统计专业学士
Olivia Hu
纽卡斯尔大学语言学专业硕士
Irene Liu
约翰霍普金斯大学国际关系/国际经济硕士
Mini Liu
东南密苏里州立大学双硕士
Shanshan Yu
英国伦敦政治经济学院金融学硕士
Stephy Tian
帝国理工化学硕士
Max Liu
帝国理工大学生物病毒学硕士
Sherry Lu
剑桥大学教育语言学硕士
Sue Pang
牛津大学经济与管理学士学位&LSE硕士
Jaryn Huang
牛津大学社会人类学专业哲学硕士
Peter Liu
牛津大学工程科学专业学士&硕士
Frances Zhu
牛津大学化学专业学士&硕士
Qianli Xia
剑桥大学数学系荣誉学士&硕士
Fang Yuan
美国普渡大学生物工程荣誉学士
Freda Yang
伦敦大学学院应用语言学硕士
Bo Su
范德堡大学英语教育硕士
Yuchen Yang
剑桥大学化学工程专业学士&硕士
Dora Liang
华威大学硕士
Tiffany Lin
伦敦大学学院经济学硕士
学习有方法，成长看得见
筑梦牛剑/G5/常春藤
唯寻导师推荐
换一换
Tiffany Lin
伦敦大学学院经济学硕士伦敦大学学院经济学硕士
· 伦敦大学皇家霍洛威学院经济学学士
· 有证券及基金从业资格证书（基础、交易、分析、承销）
· 曾就职于北京银行上海分行、西南证券等金融机构
· Tiffany老师教学严谨，细心
热门标签
唯寻导师访谈
沪ICP备18045704号-4 |
沪公网安备 31010502004453号
隐私安全
成功提交后我们将尽快与您联系，请注意来电哦！
微信咨询
成功提交后我们将尽快与您联系，请注意来电哦！
成功提交后我们将尽快与您联系，请注意来电哦！
