新2020AMC真题解析 还不快来对答案

今年国内热度超高的AMC已经考完啦，为你整理了2020AMC真题解析，快来对答案，看看自己是否过线有望吧。

（篇幅所限，本文只分析前十道2020AMC真题，完整版解析敬请关注本站）

（点击阅读热知识：AMC数学竞赛是什么 以下就能考的美国权威竞赛）

2020AMC题目分析

AMC（American Mathematics Competition）是由美国数学协会MAA于1950年成立。课程分为AMC10（针对国际学校10年级以下学员）、AMC12（针对国际学校12年级以下学员）等多个组别。当年获得AMC10前2.5%和AMC12前5%的同学可以参加当年3月的AIME邀请赛。

2020AMC真题解析（1-10）

Q1

Luka is making lemonade to sell at a school fundraiser. His recipe requires 4 times as much water as sugar and twice as much sugar as lemon juice. He uses 3 cups of lemon juice. How many cups of water does he need? (        )

卢克正在制作柠檬水以在学校筹款活动中出售。 他的食谱需要 4 倍于糖的水和 2 倍于柠檬汁的糖。 他用了 3 杯柠檬汁。 请问他需要多少杯水？

A. 6     B. 8     C. 12     D. 18     E. 24

（Difficulty Level:☆, Algebra - Fractions）

Solution    E

The ratio of water to sugar to lemon juice in general is 8 : 2 : 1. So if 3 cups of lemon juice used, 8 x 3 = 24 cups of water would be needed.

Q2

Four friends do yardwork for their neighbors over the weekend, earning 15 dollars, 20 dollars, 25 dollars, and 40 dollars, respectively. They decide to split their earnings equally among themselves. In total how much will the friend who earned 40 dollars give to the others? (        ).

A.5 dollars   B.10 dollars   C.15 dollars 

D.20 dollars  E.25 dollars

（Difficulty Level:☆, Algebra - Mean Calculation）

Solution    C

The average is

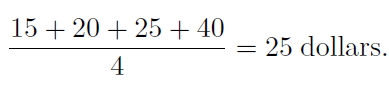
Thus the person with 40 dollars would redistribute 40 - 25 = 15 dollars.

Q3

Q3. Carrie has a rectangular garden that measures 6 feet by 8 feet. She plants the entire garden with strawberry plants. Carrie is able to plant 4 strawberry plants per square foot, and she harvests an average of 10 strawberries per plant. How many strawberries can she expect to harvest? (        ).

A. 560     B. 960     C. 1120     D. 1920    E. 3840

（Difficulty Level:☆, Algebra - Four Operations）

Solution    D

There are 6 x 8 = 48 square foot, and hence 4 x 6 x 8 = 192 plants. Consequently 192 x 10 = 1920 strawberries does Carrie harvest.

Q4

Three hexagons of increasing size are shown below. Suppose the dot pattern continues so that each successive hexagon contains one more band of dots. How many dots are in the next hexagon? (        ).

A. 35     B. 37     C. 39     D. 43     E. 49

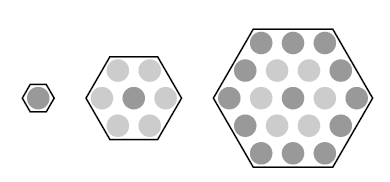
（Difficulty Level:☆, Geometry- Pattern of Shapes）

Solution    B

Except the very center, moving to a next hexagon includes one more band of dots, i.e. the fourth graph would include a fourth layer, yielding (4 - 1) x 6 = 18 new dots.

In total, 1 + (2 - 1) x 6 + (3 - 1) x 6 + (4 - 1) x 6 = 1 + 6 + 12 + 18 = 37.

Q5

 Three fourths of a pitcher is filled with pineapple juice. The pitcher is emptied by pouring an equal amount of juice into each of 5 cups. What percent of the total capacity of the pitcher did each cup receive? (        ).

A. 5     B. 10     C. 15     D. 20     E. 25

（Difficulty Level:☆, Algebra - Fractions）

Solution    C

Equally distribute three quarters into five cups.

Q6

Aaron, Darren, Karen, Maren, and Sharon rode on a small train that has five cars that seat one person each. Maren sat in the last car. Aaron sat directly behind Sharon. Darren sat in one of the cars in front of Aaron. At least one person sat between Karen and Darren. Who sat in the middle car? (        ).

A. Aaron     B. Darren     C. Karen     

D. Maren     E. Sharon

（Difficulty Level:☆, Combinatorics - Reasoning）

Solution    A

Obviously Maren is not the person (the very last position).

Since Aaron sat directly behind Sharon, they could be considered as a small team. Now Darren sat somewhere in front of Aaron, it turns out to be

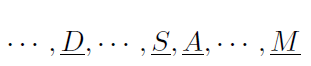
where the dots indicate possibility of other people. Now at least one person sat between Karen and Daren, thus Karen could only be the second to the last, indicating

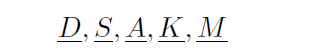
Q7

How many integers between 2020 and 2400 have four distinct digits arranged in increasing order? (For example, 2357 is one such integer.) (        )

A. 9     B. 10     C. 15     D. 21     E. 28

（Difficulty Level:☆, Combinatorics - Permutation and Combination Numbers）

Solution    C

In strictly increasing order digits, such number must start be 2300 to 2399, i.e. only 3 could be the hundred digit. Thus it remains to pick two distinct numbers from 4 to 9, with natural order we don’t need a permutation.

Note that there are 9 - 4 + 1 = 6 digits.

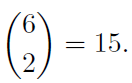
Q8

Ricardo has 2020 coins, some of which are pennies (1-cent coins) and the rest of which are nickels (5-cent coins). He has at least one penny and at least one nickel. What is the difference in cents between the greatest possible and least possible amounts of money that Ricardo can have? (        ).

A. 8062     B. 8068     C. 8072     D. 8076

E. 8082

（Difficulty Level:☆, Algebra - Four Operations）

Solution    C

Let’s figure out the greatest and least possible amount of money. Since at least one penny and at least one nickel, the greatest amount would be the case where one penny and all the rest nickels; and least amount would be the cases where one nickel and all the rest pennies. Hence

(5 x 2019 + 1) - (1 x 2019 + 5) 

= (5 - 1) x 2019 + (1 - 5)

= 4 x 2019 - 4

= 4 x 2018 = 8072.

Q9

Akash’s birthday cake is in the form of a 4 x 4 x 4 inch cube. The cake has icing on the top and the four side faces, and no icing on the bottom. Suppose the cake is cut into 64 smaller cubes, each measuring 1 x 1 x 1 inch, as shown below. How many of the small pieces will have icing on exactly two sides? (        ).

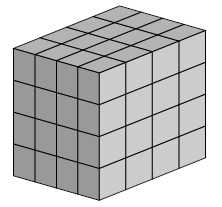
A. 12     B. 16     C. 18     D. 20     E. 24

（Difficulty Level:☆, Geometry - Surface Areas of Solid Figures）

Solution    D

Exactly two sides have icing means they are the units on the edges but not the top corners (only top corners have three sides). BE CAREFUL the bottom corners have two sides as well. Therefore, two on each of the top edges, and three on each of the side edges

4 x 2 + 4 x 3 = 20.

Q10

Zara has a collection of 4 marbles: an Aggie, a Bumblebee, a Steelie, and a Tiger. She wants to display them in a row on a shelf, but does not want to put the Steelie and the Tiger next to one another. In how many ways can she do this? (        ).

A. 6     B. 8     C. 12     D. 18     E. 24

（Difficulty Level:☆☆, Combinatorics - Counting Principles）

Solution    C

By complement, first there are 4! = 24 ways to arrange all without restrictions. Next the cases where Steelie is next to Tiger are counted as 

2! x 3! = 12

by grouping them together. Their bundle with the other two forms 3! arrangements, and 2! as a factor of themselves arranged in the bundle.

Therefore the complement is

24 - 12 = 12.

以上就是对部分2020AMC真题的解析，大家看下来觉得自己考得如何呀。AMC的小伙伴可以松一口气了，AMC10/12的小伙伴则要进入复习状态了。

竞赛的难度不容小觑，如果你不想浪费宝贵的复习时间，希望大大提升夺奖几率，点击报名【竞赛复习班】，知名大学海归竞赛导师带班，梳理考点，训练考试技巧，启发竞赛思维，帮你找到属于你的解题思路与方策略。

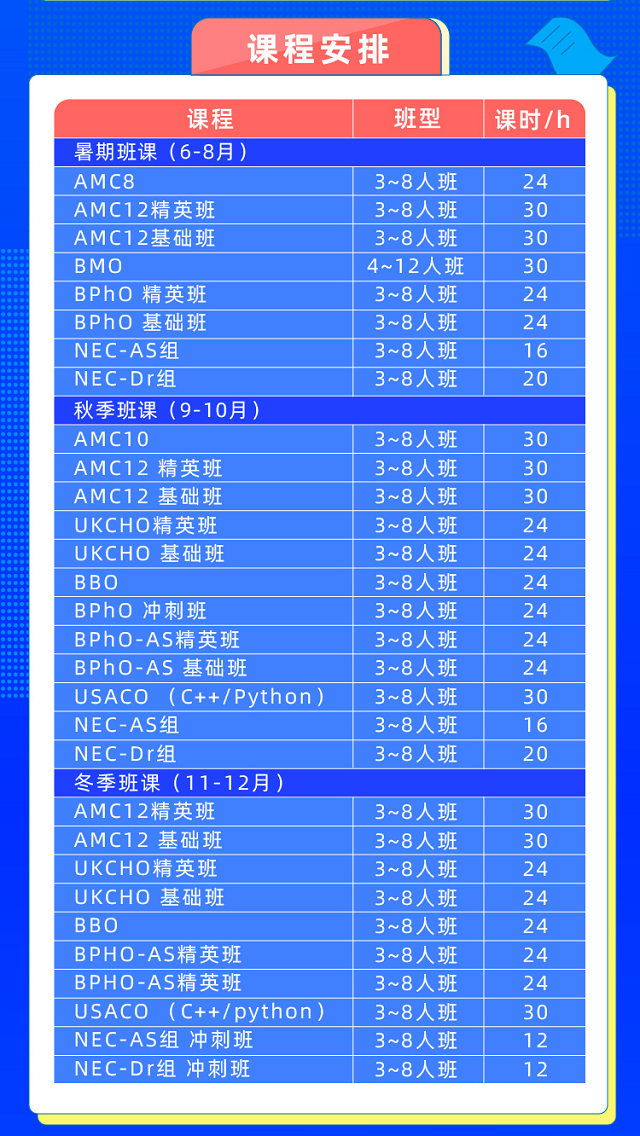
更多AMC复习攻略点击

2021AMC10竞赛2月后开考 如何复习才能助力拿奖    

amc美国数学竞赛冷门攻略 IB和AP学员重点收藏    

扫码添加小唯

你的专属留学管家