还有不到2个月就是AMC10的竞赛考试了，这时候同学们一定都在紧张的复习，下面给大家带来一些被称为史上最难的AMC10真题解析，以及一些有关几何问题的讲解，复习的同学赶紧看看哦。
AMC10真题解析
解析：
真题
解析：
解析：
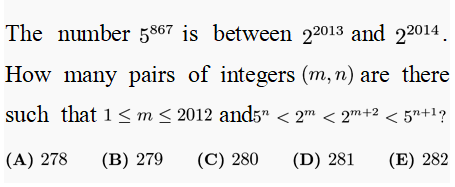
解析：
AMC10竞赛几何部分讲解
词汇
centroid (center of mass): 质心/重心
line segment: 线段
intersection: 交点
right triangle: 直角三角形
hypotenuse: 直角三角形的斜边
rectangular coordinate system: 直角坐标系
slope: 斜率
perpendicular: 垂直
parallel: 平行
vertex (vertices): 顶点
求解几何问题
今天介绍的利用直角坐标系求解的几何问题涉及三角形的重心。
三角形的重心是三角形三条中线的交点。重心的主要性质有：
重心到顶点的距离与重心到对边中点的距离之比为2:1。
重心和三角形3个顶点组成的3个三角形面积相等。
在直角坐标系中，重心的坐标等于三角形三个顶点坐标的算术平均。
2018年AMC10B的12题
这个题问的是三角形重心的运动轨迹所覆盖区域的面积大小，如果单纯从平面几何入手，很难想象出重心的运动轨迹是什么。所以这时候就可以利用平面直角坐标系来帮助解题。
假设以线段AB的中点为原点，线段AB所在的直线为x轴建立直角坐标系，那么可以得出A(-12,0), B(12,0), C(x,y)。
根据重心的第三个性质，则三角形ABC的重心的
x坐标为(-12+12+x)/3=x/3,
y坐标为(0+0+y)/3=y/3.
因为ABC三个点在圆上，所以圆的方程为x^2+y^2=144.
从而得出重心所满足的方程为(x/3)^2+(y/3)^2=144/9.也就是说重心的运动轨迹是一个圆心在原点，半径为4的圆。那么题目所求的面积=16π≈50
看了以上的介绍同学们有没有对AMC10竞赛难度有了新的认识呢？竞赛考验的是同学们对于数学能力的应用以及逻辑思维的发散，这些都是需要经过训练的。在2019年与2020年的AMC竞赛中，唯寻均有收获，如果你也想手拿奖项，欢迎您点击【预约试听】报名参加唯寻竞赛复习班。
更多竞赛复习信息，点击
如何准备美国数学竞赛AMC10 先把这些AMC10考点分析熟记于心对症下药才能拿到奖项
换一换
沪公网安备 31010502004453号
成功提交后我们将尽快与您联系，请注意来电哦！
成功提交后我们将尽快与您联系，请注意来电哦！
