牛津MAT真题分析与讲解 报考英国数学专业真题可是很重要的复习资料

今年的牛津申请至此就要落下帷幕了，牛津申请还是具有一定的难度的，下面给大家带来了2019年的牛津MAT真题讲解，如果你打算申请英国优质大学的数学专业，这些真题就十分重要哦！

解析：数形结合，等式左边为一元三次函数，右边为水平线，算出极值点处的函数值，即可得到答案

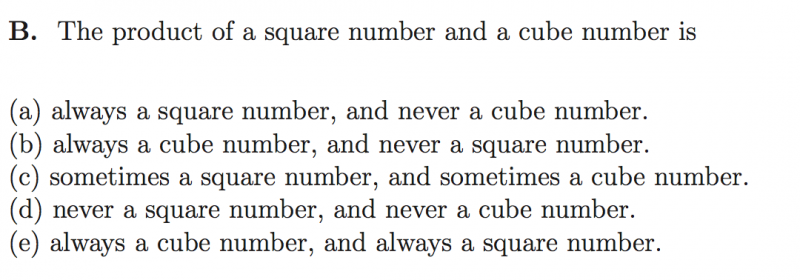
解析：取特殊值法，1，4，8，27可以组合判断出

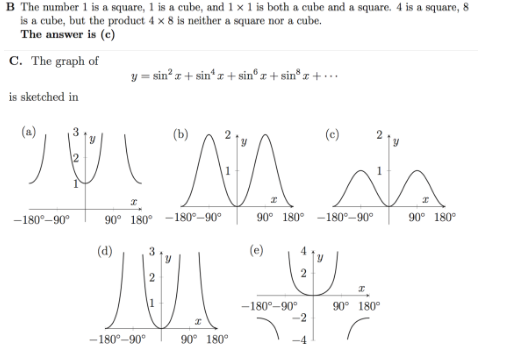
解析：求和等式为等比数列，根据求和公式化简到最简形式，是正切值的平方，只能取非负数，再根据正切函数性质得到答案

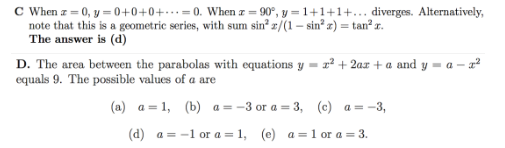
解析：数形结合，因不知道a取值正负，画出2幅不同图像相交，分别位于第二和第四象限；然后根据积分求面积建立等式求解

解析：根据三角函数恒等式化简，得到x,y的正弦值等式，进而得到无穷多解

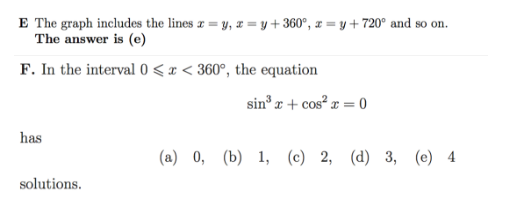
解析：通过三角函数恒等式建立关于正弦值的一元三次方程，求导得到极限值然后进行判断，在给定定义域有三角函数值即可判断解的个数

解析：根据前2个对数方程得到c的值，然后再根据第3个方程构造关于a,b的方程，数形结合画出图像即可得到答案

解析：根据实际意义可以排除正切值为负值，数形结合根据等比数列公式得到公比方程，求解一元二次方程即可

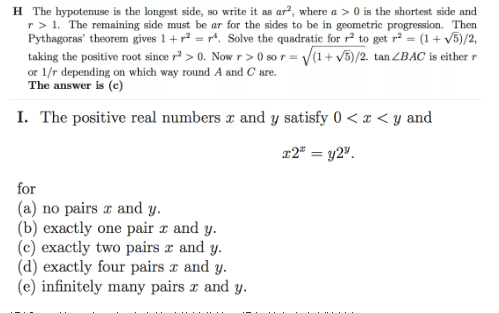
解析：两边同时取以2为底的对数并化简，根据给定定义域判断

解析：根据等边三角形性质，三线共点切分边长比例为2:1，最短距离的线段和平行于边长的直线共线，故长度也满足比例式

解析：(i)阶数和幂函数最高项有关，相乘根据等差数列求和公式求解；

(ii)代入特殊值，建立关于k和系数项的方程，适当缩小法得到不等式；

(iii)根据题干可知，当幂函数阶数不断增加时，因为高阶幂函数只会影响高阶，因低阶不再进行运算处理，故对匹配的系数不再有影响

(iv)根据题干提示代换因子重写等式，然后两边同乘图片等式保持不变，即可得到相类似的等式；

(v)根据(ii)结论，一共有N+1项系数，其中最大系数不小于图片，根据学员猜想如果成立的话，最大系数不大于N+1.构造出不等式可以推出矛盾，因指数变化永远比幂函数快，故学员猜想错误

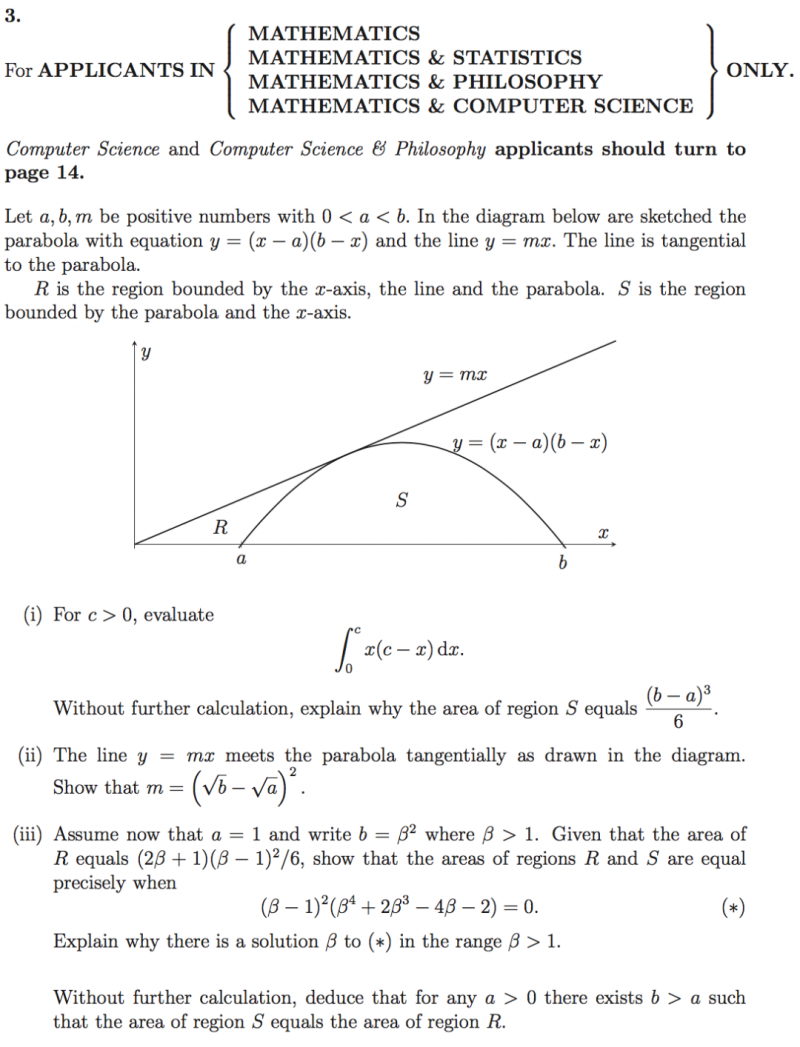
解析：(i)根据幂函数积分公式得到一般解，如果设c=b-a.可以观察出题干被积函数为图像左右移动得到，面积相等；

(ii)直线和曲线相切，两者联立方程可得到一元二次方程，判别式为0，可以得到要求证明等式

(iii)根据题干和(i)问结论可得到等式，然后合并处理即可得到要求证明等式；通过观察等式可知，存在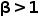使得等式成立；根据前面做题过程可以得到面积相等所对应的值

解析：(i)根据题干提示可知，给定点在定义域里面即为该点，给定点在外面的话就要除以它的模长，可以根据圆的定义去判断；

(ii)如果给定S为开区间，给定点位于圆外的话，则没有确定点距离最近，因为边界值取不到

(iii)根据圆的定义，给定点为圆心，给定区域为圆的话，圆上无数点到圆心距离最近；

(iv)根据两点间距离公式，可以构造关于x的一元二次方程，因2次方系数为正值，开口朝上有最小值

(v)根据给定S定义，还原回x,y关系式可得，定义域为直线，所以整条直线为给定区域

(vi)根据(iv)问结论，可知在顶点处取最小值且只有一个，故推出不能有2个不同点

解析：(i)根据题干可知，每个子集包括至少2个元素，根据特殊情况，如果每个子集都是2个，可知整体元素超过给定元素和n，因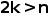

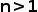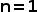(ii)分或者讨论，当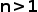时，只有1个子集，当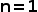时，没有子集满足题干

(iii)按照题干要求，依次构造需要情况，取出2个元素之后，剩下的n-1个元素进行组合,学员注意在挑选任意一个时有n种选择，这样对于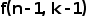来说就可以重复n遍，同时学员留意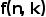因为k的值不，每次内部分割时，不同分割情况也相当于情况重复

(iv)根据(iii)问的递推关系提示，将需要的部分组合出来即可

(v)借鉴(iii)问结论，讨论2n+2,2n+1,n+1,2n特殊情况进行公式整理，，注意元素个数变为2n+1个

以上就是MATz真题了，近几年参加MAT的人数越来越多了，如何在这些前置性测试中考出高分呢？除了需要提前准备，找到一位懂得答题套路的导师也是非常重要的，唯寻集结了一批来自牛津剑桥毕业的导师，用他们亲身经历，教你快速答题。想提前锁定牛津吗？赶紧点击【预约试听】参加牛剑笔试车。

点击

同为数学考试STEP和MAT究竟该考哪个

牛津大学MAT考试难度以及复习建议

查看更多。