本期想来给大家分享IB数学麦克劳林公式，这个公式注重对同学们的逻辑能力的考察，下面就一起来看看具体的知识点吧！
麦克劳林公式是一个数学国际课程的专业术语，指泰勒公式（在x=0下）的一种特殊形式，麦克劳林公式是泰勒公式在0点展开的特例。
注：泰勒公式：在数学中，泰勒公式是一个用函数在某点的信息描述其附近取值的公式。如果函数足够光滑的话，在已知函数在某一点的各阶导数值的情况之下，泰勒公式可以用这些导数值做系数构建一个多项式来求近似函数在这一点的邻域中的值。泰勒公式还可以给出这个多项式和实际的函数值之间的偏差。
麦克劳林公式的作用是把函数近似表达为一个多项式。但在使用的时候要考虑精度，也就是对给定函数展开到多少阶的问题。
运用
一般情况下遇到的极限有两种情况：
（1）分子是两个或者以上的函数相加减，这种情况比较简单，只要将两个函数展开到与分母同阶即可
（2）分子是两个或以上的函数相乘，这种情况比较复杂，主要考虑的是分子相乘会出现的所有与分母同阶的项，举个例子，比如分母是三阶，那么两个多项式必须都展开到三阶，因为一个函数的常数项与另一个函数的三次项，一个函数的一次项与另一个函数的二次项相乘都是三次，也就说，必须要助力展开的阶数相乘会得到所有与分母同阶的三次项。
常用的麦克劳林公式
函数展开成泰勒级数的充要条件
设f(x)在x0的某个领域内具有各阶导数，则f(x)在该邻域内能展开成泰勒级数的充分必要条件是当阶数无穷大时f(x)的泰勒公式中的余项趋向0，此时函数f(x)可以展开为泰勒级数：
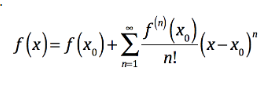
IB数学无论是在平时的教学中还是考试的要求中，也更强调解决问题的逻辑和方法。
和ALEVEL数学一样，想申知名大学，IB数学都是要奔满分去的。如果担心一开始无法适应IB压力大，节奏快的学习特点，可以利用summer vacation预习起来，欢迎点击了解【唯寻IB暑期先修班】——
点击
查看。
快扫码
关注老师微信
潘田翰(创始人)
剑桥大学化学工程硕士
Candise Cai
牛津大学化学硕士
Chris Chen
帝国理工学院物理学士
Ruby Rui
剑桥大学经济系学士&双硕士学位
Elaine Xu
牛津大学数学与统计专业学士
Olivia Hu
纽卡斯尔大学语言学专业硕士
Irene Liu
约翰霍普金斯大学国际关系/国际经济硕士
Mini Liu
东南密苏里州立大学双硕士
Shanshan Yu
英国伦敦政治经济学院金融学硕士
Stephy Tian
帝国理工化学硕士
Max Liu
帝国理工大学生物病毒学硕士
Sherry Lu
剑桥大学教育语言学硕士
Sue Pang
牛津大学经济与管理学士学位&LSE硕士
Jaryn Huang
牛津大学社会人类学专业哲学硕士
Peter Liu
牛津大学工程科学专业学士&硕士
Frances Zhu
牛津大学化学专业学士&硕士
Qianli Xia
剑桥大学数学系荣誉学士&硕士
Fang Yuan
美国普渡大学生物工程荣誉学士
Freda Yang
伦敦大学学院应用语言学硕士
Bo Su
范德堡大学英语教育硕士
Yuchen Yang
剑桥大学化学工程专业学士&硕士
Dora Liang
华威大学硕士
Tiffany Lin
伦敦大学学院经济学硕士
学习有方法，成长看得见
筑梦牛剑/G5/常春藤
唯寻导师推荐
换一换
Yuchen Yang
剑桥大学化学工程专业学士&硕士David Yang剑桥大学化学工程专业荣誉学士&硕士
· 伦敦优质男校德威中学A-Level A*A*A*A*A*
· 剑桥三一学院全额奖学金获得者
· 英国物理奥林匹克BPhO，化学奥林匹克UKChO金奖，均入选国家队选拔，数学奥林匹克BMO金奖
· 剑桥化学竞赛C3L6 Roentgenium奖，曾受邀于皇家科学院发表演讲
· 教学风格：注重逻辑，重点明确，课堂效率高，适合需要全面提升的学生
热门标签
唯寻导师访谈
沪ICP备18045704号-4 |
沪公网安备 31010502004453号
隐私安全
成功提交后我们将尽快与您联系，请注意来电哦！
微信咨询
成功提交后我们将尽快与您联系，请注意来电哦！
成功提交后我们将尽快与您联系，请注意来电哦！
