AMC 8真题测试来了 进来测测你与奖项还有多少距离

AMC考试已经进入倒计时了，有志于拿奖的同学们是否都掌握了考点呢？今天就以2019年的一道真题为例，来测测同学们的实际水平。这是一道组合型的题目，近年来组合体在AMC考试中占据的比例也越来越重了，同学们在考前一定要认真的复习哦。【amc美国数学竞赛冷门攻略 IB和AP学员重点收藏】

Alice has 24 apples. In how many ways can she share them with Becky and Chris so that each of the three people has at least two apples?

(A) 105

(B) 114

(C) 190

(D) 210

(E) 380

题目里在说分苹果，我们让爱丽丝分一分南瓜——假设爱丽丝（A）有24个。一共有多少种不同的分法能让她、贝蒂（B）和克里斯（C）三个人每人分到至少2个呢？看到什么题目都先别急着放弃，即便是乍一看让人束手无策的难题，我们总可以用笨办法一点一点尝试，说不定就能总结出规律。无论是笨办法还是聪明办法，能解决题目就是好办法。

 不妨试着分分看，比如我们先给爱丽丝留2个， 那么接下来该怎样给贝蒂和克里斯分呢？

爱丽丝拿走两个以后，贝蒂和克里斯瓜分剩下的22个。如果贝蒂拿2个，克里斯手里剩下20个。贝蒂拿3个，克里斯手中就剩下19个……这时候我们好像能看到一些规律了。

从这张图里可以总结出，当爱丽丝分给自己2个的时候。贝蒂和克里斯对剩下的22个南瓜可以有（20+1）-2 = 19种不同的分配方法。以此类推，当爱丽丝自己拿走3个的时候，贝蒂和克里斯可以按（19+1）-2 = 18种不同的方法分配剩余的21个南瓜……直到爱丽丝一口气分给自己20个，贝蒂和克里斯这时候就只有（2+1）-2 = 1种分配方案了。把所有方法统统加起来，即19 + 18 + 17 + … + 1 = 190，答案选C！

那么有没有更“聪明”的算法呢？聪明的你不妨开动脑筋一起思考。

现在我们让爱丽丝、贝蒂和克里斯并排坐好，再来分一次。已知每个人至少要有2个，那我们不如先给每个人分好2个，再考虑剩下的24- 2*3 = 18个。

接下来要考虑的问题就变成了：把18个分给3个人，每个人分得的数量不限。举个例子，我们可以分给爱丽丝9个，贝蒂9个，克里斯0个，毕竟每个人手里本来已经有了2个保底。

老规矩，我们画图试试。

当把排成一排的时候，我们可以发现，这个分的问题可以转化成一个简单的排列组合问题。我们实际上并不需要把 x+y+z = 18这个方程组解出来，因为我们并不在意每个人最终分到了几个。我们只想知道这个方程有多少个解。

从这张图很容易看出，每一行南瓜都是一种分法：蓝色箭头左边是爱丽丝的，两个箭头中间是贝蒂的，绿色箭头的右边是克里斯的。现在我们只需要知道有多少种不同的排列箭头和南瓜的方式。

 2个箭头，18个，所以一共有20个空位。在第一个空位里，我们有20个不同的物品可以放，第二个空位便剩下19个选择，第三个空位则是18个……这样计算下来一共有20！种不同排列方法。

 然而事实上我们重复计算了好多种。比如

以上这两种排列方法就完全没有区别。它们都代表了爱丽丝、贝蒂和克里斯分得南瓜数量是0:0:18的情况。于是在20！种不同的排列方式中，我们都重复计算了箭头2！次，也就是2次。除此之外，所有的南瓜之间也没有区别。如果我们给南瓜编号，

几号南瓜待在几号空位里并不影响最后的分配。所以在20！种不同的排列方式里，每一次我们都多算了南瓜们18！次。所以最后的结果应该是20！/（18！2！）= 190次。当然了，熟悉排列组合的读者可能一眼就能看出这是我们的选择公式，也就是20选2 = 190种。所以这道题选择C。

同学们你学会了吗？在做这些题目时一定要想到合适的排列方式选择一个最简便的方式来计算。想知道更多AMC复习技巧吗？那就赶紧来唯寻吧，唯寻的竞赛复习班的精英带你轻松拿奖。【国际学校入学考试太难 教你一招用AMC考试快速搞定】

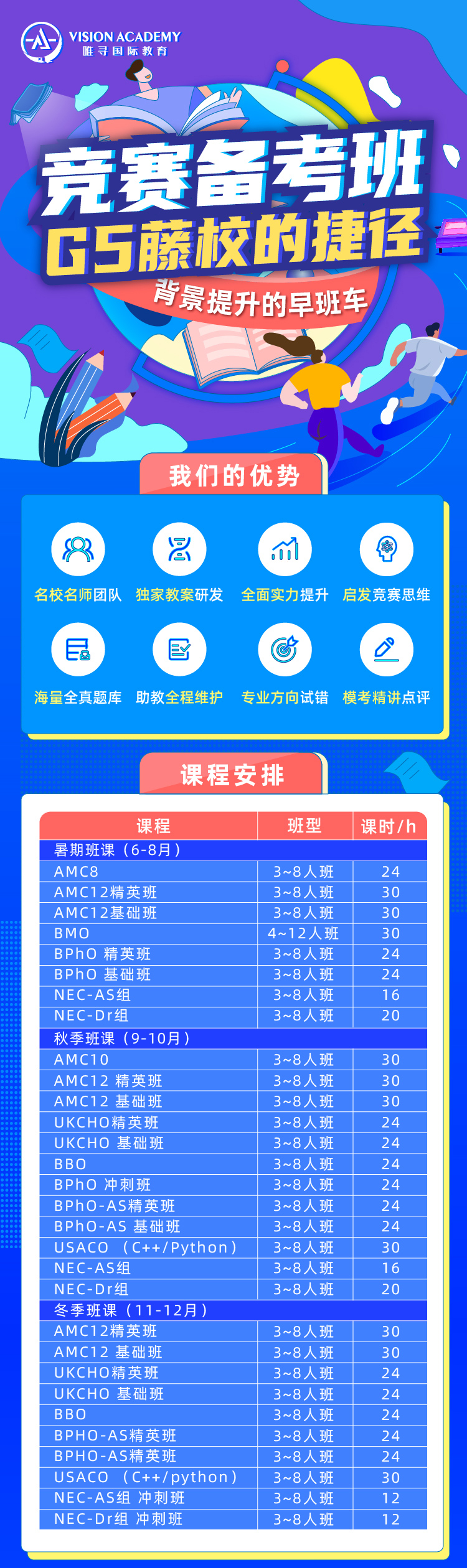
唯寻国际教育团队源自牛津、剑桥、美国常春藤等世界精英学府，专注于A-Level，IB，AP，IGCSE等国际课程全国际课程培训，并提供英美优质大学笔试面试辅导以及国际竞赛培训。