
马上就迎来了IGCSE考试了,今天给大家讲解的是IGCSE数学的导数部分,导数在整个国际学校的的数学中都占据重要的位置。同学们要怎么学习这部分的内容呢?下面让我们一起来看看导数部分的IGCSE数学真题讲解吧!
Derivative:the limit of theratio of the change in a function to the corresponding change in itsindependent variable as the latter change approaches zero.
从导数的定义中,我们不难发现,导数的概念是在微小的变化中体现的,微小到approaches 0, 也就是Δx→0。因此导数要建立在这个基础上去理解,dy/dx,就是Δy/Δx。这是纯定义上的理解,在一些证明题中需要用到这个思路。
导数的应用意义:导数也是斜率,梯度gradient,与直线方程有相关性;同时在应用题中,将与速度、加速度联系起来;二阶导数,表征方程曲线的开口方向,同时,它是一阶导数的导数,表征着一阶导数的变化情况。
考试重点:考试中,导数会考察基本函数的求导计算,同时重点是求max和min,此部分内容单独出题,较简单,如果与geometry及kinematics结合起来,将考察考生对于函数的处理能力,从应用信息中,列出函数,求取max及min(需要注意应用题取值一般大于0)。考试中出现过考察导数定义的题型,这类的题是难点,需要大家深刻理解f’(x)=dy/dx=Δy/Δx(Δx→0).
Derivative导数或者Differentiation微分,这部分的内容与line直线、integration积分、trigonometry三角函数相结合考察的概率很大,其中需要应用到derivative的几何意义。
考点:f’(x)=dy/dx=△y/△x,导数是变化率,是在一定区间内,y的变化与x的变化的比值,也是函数曲线在某点处切线的斜率,而积分主要应用在计算面积的题型中,求取max和min,是在stationary point处求得,其他的就是基本求导的计算。
首先是求导的基本计算
composite、product、division这些基本的函数求导要快速准确的计算出来。这些题也没什么解题思路,简单明了。

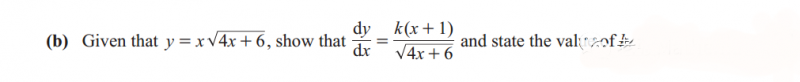
与直线方程相结合
主要是考察某点处的tangent和normal,这类题只是在基本求导后多增加一步计算,注意tangent与normal的区别。先求导,然后求斜率,最后列方程。有些题可能涉及到分析题干,列等式。
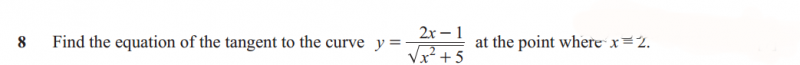
这个题是一道积分题,放到这里是让大家能够理解,函数的求导的几何意义其实就是gradient。
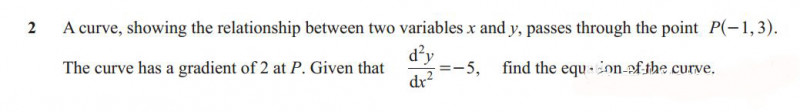
有些题会考察导数的极限含义,也就是△x趋近0这个定义。
第一步是基本求导,给出函数是一个product和composite的结合,注意求导的计算。第二步,计算△y,f’(x)= △y/△x,因此△y=f’(2)* △x,△x也就是0.03。这是对定义的考察,需要从函数曲线上去加深理解。
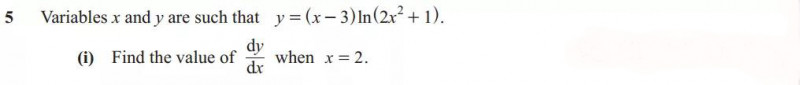

Derivative还可以与integration结合,先求取曲线的方程,然后计算阴影部分的面积,这类题比较综合,但将题干肢解,细心计算每一步并不难,需要勤加练习。
以上就是给同学们讲解的有关IGCSE数学导数的一些知识了,同学们如果有需要的话可以自己去做一下以上这几道题,然后可以跟我们的导师联系哦,看看自己是否能够将这几道题全都做对。想了解更多IGCSE真题吗?那就赶紧点击【预约试听】了解更多吧!

更多信息点击
或者扫描下方二维码了解更多。


学习有方法,成长看得见
筑梦牛剑/G5/常春藤
