IB数学SL知识点讲解 向正确解出切线方程还得靠导数

马上就是winter vacation了，但是同学不能放松自己对于课程的复习哦，因为IB大考一紧近在眼前了，今天给大家讲一个IB数学SL中比较重要的知识点切线方程。想找到解方程的便捷方法吗？那就赶紧来听听本日的IB数学SL知识点讲解吧！

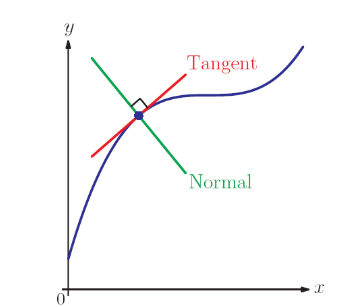
tangent切线：A tangent is a straight line which touches the curve without crossing it.

切线是与曲线只有一个交点的直线，需要注意的是，切线是对于曲线上某一点而言的，在延伸的范围内，切线与曲线可以有其他交点。

重点：数学语言解读，the derivative of a function f(x) is another function that gives the gradient of y=f(x) at any point in the x domain.曲线在某一点的导数与在这一点的切线的斜率相等。因此，我们掌握了求切线方程的第一个关键要素：利用导数求切线斜率。

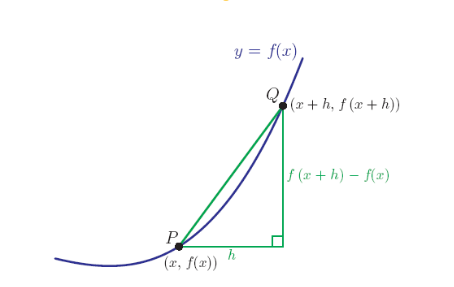
gradient斜率：是在straight line，也就是SL2.1中的内容，m=（y2-y1）/（x2-x1），也就是对应两点横纵坐标差的比值，同时，从图上看，这个比值也是PQ与横坐标夹角的tangent值（对边/临边）。两种特殊的情况，水平直线：y=c，斜率为0，垂直直线：x=c，斜率为∞。

straight line equation直线方程：表达直线方程有多种形式，

（1）gradient-intercept form：y=mx+c；

（2）general form：ax+by+d=0；

（3）point-gradient form：y−y1=m(x−x1).

在实际的解题过程中，熟练运用第三种形式，也就是point-gradient form是较为通用的方式，同时注意，一般做题过程中，需要将equation化简成（1）或（2）的形式，而（1）的形式在更多的mark sheme中被用到。

normal法线：切线与法线是互相垂直的关系perpendicular，因此，m1*m2=-1，在得到切线斜率之后，也就可以求取法线斜率。而对于平行直线parallel，m1=m2，斜率相等。

Method marks解题点：求取切线或法线方程是导数应用的重要内容，在guide中明确写道Use of both analytic approaches and technology.具体的解题步骤可概括如下：

a.求导函数f’(x)，利用已知f(x)，通过differentiation求取函数的导函数；

b.代入点P坐标，求导数，即点P处切线的斜率gradient，如果求法线方程，利用m1*m2=-1，求法线斜率；

c.确认P点坐标，如果仅给P点横坐标，需要代入f(x)中，确认P点坐标（x，y）；

d.已知P点坐标（x，y）及过P点切线斜率m，利用y−y1=m(x−x1)求取line equation，记得化简。

这是出题思路最简单的形式，同样的知识点，还可以有复杂的出题形式，包括f(x)复杂化，增加导数求取的难度；将f(x)中某一参数设为未知项，给出斜率，确认参数值等其他的出题形式。但是，无论哪一种形式，都可以通过以上的步骤，构建方程，并求取最终的结果。

以上就是IB数学有关切线方程的信息了，同学们如果您对这部分的知识点还有其他疑问，欢迎您前来唯寻，唯寻IB课程

学术背景深厚的导师更能为IB学员

提供有发散性和辩证性的学术指导

精讲学校不强调的高分论文要求与调查访问手段

唯寻每年服务国际学校学员

复习经验更有保障

点击

IB改革后IB数学选课选错会被目标大学拒绝？附G5院校对于IB数学选课要求

IB数学真题解析这几道代表性的数学题你都学会了吗

查看。