IB数学真题解析这几道代表性的数学题你都学会了吗

不管对哪个课程体系的同学们来说，数学都是让人非常头疼的，想要数学成绩考得好，真题复习必不可少，那么本期唯寻就给大家带来几道IB数学以及解题方法，同学们在观看的同时一定要举一反三，思考有无其他的解题方法。

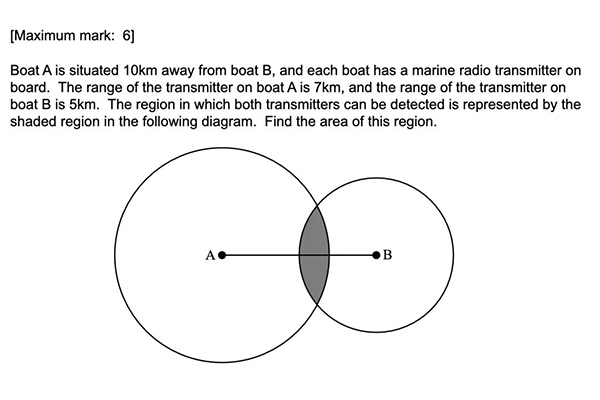
一道来自于2018年11月Mathematics HL P2 Section A的一道经典的求扇形和三角形面积的题目。根据题干可知，这道题目是两个半径不同的圆有重叠，并求重叠部分（阴影画出）的面积。想要求出阴影部分面积，就要通过扇形与三角形部分的面积加加减减来计算了。

将原题的已知线段长度标出，并将⊙A和⊙B的两个交点标记为点C 与点D。

阴影面积 = 扇形ACD面积 + 扇形 BCD面积 - 三角形ACD面积 - 三角形BCD。要想算出任意面积，∠CAD与∠CBD的大小都是需要求得的。既然已知AC，AB，CB的长度，那我们就可以利用cosine rule  计算出∠CAB和∠CBA的大小。

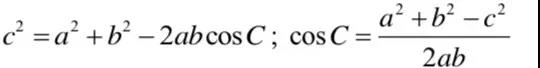
算出∠CAB和∠CBA的大小后，我们就可以直接计算扇形与三角形的面积了。

利用Math Formulae Booklet中这两个公式来计算。

计算两个扇形的面积：

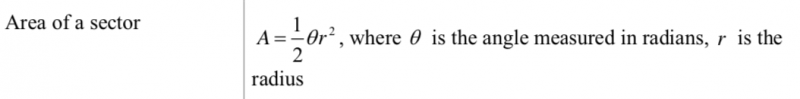
计算两个三角形的面积：

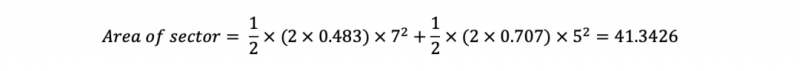
两个部分的面积相减，就可得到8.85的答案了！

2、是一道排列组合的经典大题，这道题主要的考点是排列（permutation），从n个不同元素中取出m（m≤n）个元素，按照一定的顺序排成一列，叫做从n个元素中取出m个元素的一个排列。题目非常的直截了当，告诉我们一共有14个座位，8个病人，

(i) 这一小问的条件题目已经直接给我们了，即m=14，n=8，所以我们根据条件可得14P8=14！/6！=121080960 注：需要排列的仅是八个病人，剩下的6个空位置并不需要进行排列。

(ii) 这一小问的题目也没有绕圈子，说其中3个人是一家人，他们要坐在一起。首先我们可以先考虑这一家庭之外的排列。所以这题的m=14-3=11，n=8-3=5，即11P5=55440。接下里我们考虑这一家人的排列，3个人一共有3P3=6种排列，然后这一家人的位置可以在头尾还有11个位置之间即2+10=12，所以总的排列即是：这家人内部的排列×这家人所在的位置×他人的排列=6×12×55440=3991680.、

(iii) 第（iii）小问则需要从两方面入手：①咳嗽的病友两边都是空位的排列 ②病友坐在头和尾，且旁边空着一个座位的排列。

种情况：在第二题中就提示过我们可以把一个家庭看作一个整体，则这一问也可以把病友和两个空位置看作一个整体，区别就是没有内部的排列，因为病友只有一个人。所以这问的m=14-3=11,n=8-1=7,11P7=1663200,接下来就是这个病友还有这两个位置合起来的这个组合能放在12个位置（头尾+11个位置的中间），所以种情况的排列=12×1663200=19958400

第二种情况：当病友在头尾，且旁边空着一个位置。这题的m=14-12=12,n=8-1=7

12P7=3991680, 所以这种情况的排列=2×3991680=7983360

两种情况相加即可得本题得答案：19958400+7983360=27941760

以上这两道都是非常经典的IB数学题，看完了唯寻教学团队给出的解题方法，不知同学们还有其他的解题方式吗？数学是一个非常有趣又实用的国际课程，想要学习数学或者有其他IB课程辅导需求的，都可以前来唯寻。

更多IB数学信息，点击【ib数学补习6大原则 你都清楚吗】、【想攻克IB数学排列组合？ 快收下这5个组合公式】即刻查看。