IB物理考纲Topic 1详细梳理，别让简单内容成为丢分大坑

测量与不确定度（Measurements and uncertainties）是IB物理考纲（HL&SL）的第一个主题，由于这个TOPIC本身非常基础，很多同学翻一下就当复习完了，如果有1、2个不确定的点也会想着以后再复习也来得及。但往往最基础的知识才会决定你能不能拿7分，如果不想无辜送分，最好还是踏实过一遍。所以本文就为大家分享一下IB物理考纲这个主题的详细梳理。

（点击阅读IB物理真题解析）

IB物理课程简介

IB物理有HL和SL之分，SL学习的是核心内容，HL则需要在SL基础上再学习一些拓展知识，大学想申请理科类专业的同学建议选修HL物理。

在课程内容方面，国内物理更加重视对经典力学和电磁学等知识内容的学习，而IB物理则更加关注与人们生活息息相关的物理学内容。
IB物理考纲的知识范围更加广泛，比如全球气候变化、电子技术，天体物理学、粒子物理等内容都在学习范围内。

国内物理偏重于纵向挖掘，学习的比较深，且侧重于培养计算分析能力；而IB物理重视横向拓展，学习的范围更广，侧重于培养学员思考和观察能力。

IB物理考纲Topic1整理

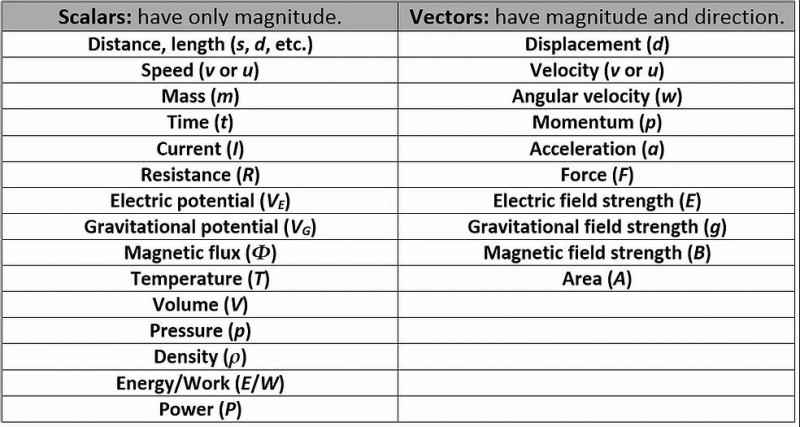
Topic 1的学习内容主要有测量与不确定性：包括测量、不确定性和误差、标量和矢量等。

Topic 1：Measurements and Uncertainties

1.1 Measurements in Physics

▲ Fundamental and derived SI units
计量的基本单位是国际单位制（SI，即International System of Units ），这些单位组成了派生单位，例如牛顿（N）。
基本单位主要包括：

Length: metre (m)

Mass: kilogram (kg)

Time: second (s)

Electrical current: ampere (A) 

Temperature: kelvin (K)

Amount of substance: mole (mol)

Luminous intensity: candela (cd) 

▲ Metric multipliers and scientific notation
● 公制乘数：对应10的幂，例如，kilo (k) - 10³。

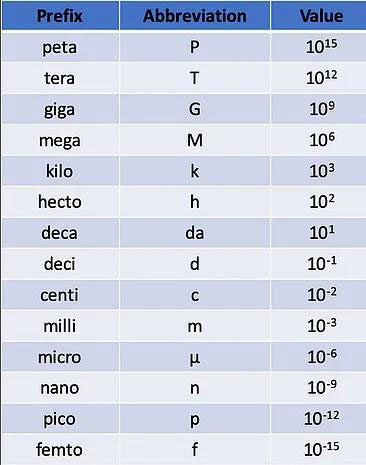
● 科学计数法：表示太大或太小数字的便捷方法。
表示法：mx 10 ^ n，其中1≤m<10，并且 n 是整数（正数或负数）。
例如：213000000 = 2.13 x 10 ^ 8
● 数量级：将数字近似为最接近的10的幂。
重要数值的数量表：

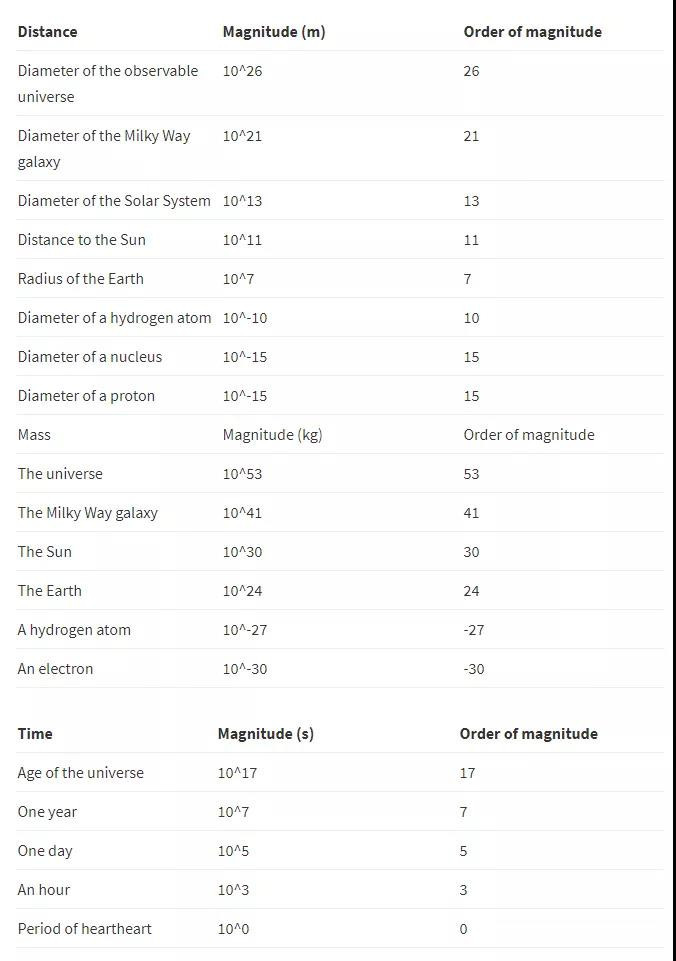
● 估算值
通常以最接近的10的幂进行估算。例如：0.0000945≅10 ^ -4
▲Significant figures (s.f.) 
有效数字用于表示实际能够测量到的数字。能够测量到的是包括最后一位估计的、不确定的数字，展示数据的度，用s.f.表示。
● 计算有效数字的规则：

非零数字始终有效。例如：1234 - four s.f.

数字中间的夹零始终有效。例如：5403 - four s.f.

左边的零点永远都无效。例如：0.0004578 - four s.f.

只有在有小数点的情况下，右边的零才有意义。例如：1403.00000 - nine s.f.

●数字的四舍五入规则：
如果最后一位有效数字后的数字小于5，则该数字保持相等，例如，将678.4（4 s.f.）舍入为3 s.f. = 678。
如果在最后一个有效位的数目大于5，则数字向上计入（即入1），例如678.6（4 s.f.）舍入到3s.f. = 679。
如果最后一个有效数字后的数字是5，并且后面仅跟零这个数字：
■ 最后一个有效数字为小于5的数字，则向下舍去，例如3.2500（5 s.f.）舍入为2 s.f.= 3.2。
■ 最后一个有效数字为大于5的数字，则向上入1，例如3.35 00（5 s.f.）四舍五入到2 s.f.= 3.4。 

1.2 Uncertainties and Errors

▲ Errors (or uncertainties) in experimentation
所有的测量是真正数值的大约值，因为总会存在误差：
● 系统误差：将测量偏向同一方向，例如始终为+0.1 cm。
产生原因：设备校准不充分；忽略了摩擦的影响（假设其是恒定的）等。
● 随机误差：测量结果向各个方向倾斜，导致误差的广泛分布。
产生原因：手动使用秒表，某些测量值（时间）将高于实时数值，而某些测量值将低于实时数值；变化的外部环境， 如变化的大气条件等。
● 解决方案：收集各种值，然后取平均值。
▲ Accuracy  and precision:
● Accurate measurement：低系统误差，平均值接近实际值。
● Precise measurement：低随机误差，数值彼此接近。
▲ Errors (or uncertainties) in measurements
仪器中随机误差的估计：加减误差。不确定度应始终具有相同数目的小数位作为值来测量，并且通常只1 s.f.。
●数字仪器（例如秒表）：可能的最小刻度宽度，即仪器可以读取的最小刻度。
示例：秒表显示的数值

最小值距：0.01秒
不确定度：± 0.01 s
值：8.78 +-0.01 s
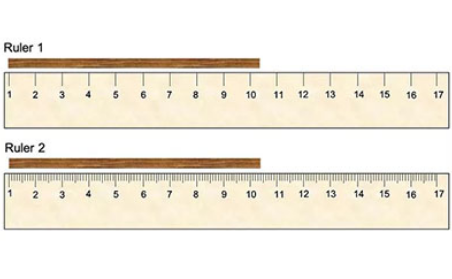
● 类比仪器 （如直尺）：取整的最小可能值距

■ 标尺1： 
最小值距：1 cm
不确定度：+- 0.5 cm
值：12.5 +- 0.5 cm
■ 标尺2：比标尺A更。
最小值距：0.1 cm
不确定度：+- 0.05 cm
值：12.50 +- 0.05 cm 

▲ Errors (or uncertainties) in calculations
以下值：L1: 8.3 +- 0.1 cm为例。
■ Absolute uncertainty 不确定度（ ∆x ）：具有与值相同的单位，例如L1：±0.1 cm
■ Fractional uncertainty 分数不确定度：不确定度与值本身相除，例如对于L1：0.1 / 8.3 = 0.012
■ Percentage uncertainty 百分比不确定度：百分比不确定度乘以100％的乘积，例如L1：0.012 x 100％= 1.2％
▲ Propagation of uncertainties:
■ 加法或减法：值的加法或减法以及不确定度的加法。
示例：L1-L2：（8.3±0.1）-（7.4±0.5）= 0.9±0.6cm。
■ 乘除法：数值的乘法或除法另外分式不确定度或百分比的不确定度。
例如：L1 x L2: (8.3 +- 1.2%) x (7.4 +- 6.8%) = 61 +- 8.0% cm²。
■ 数的乘方和开方：数值的乘方和分数的不确定度或百分比的不确定度的乘方值。
例如：L1³：（（8.3 +-1.2％）^ 3 = 570 + -3.6％cm³。
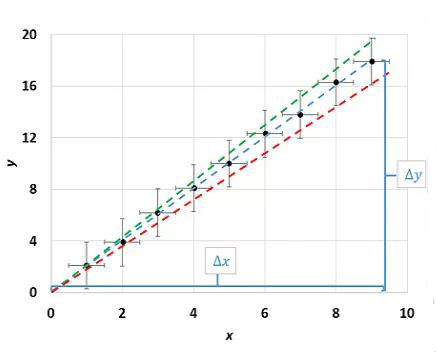
▲ Errors (or uncertainties) in graphs
误差框：
图表中一个值的不确定度通常用误差线表示。
误差y值因x值的不同而不同。

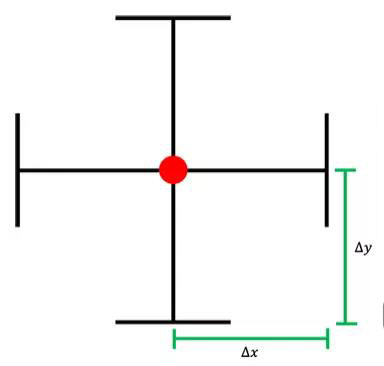
 ■ 最佳拟合线：穿过所有误差线的线（不一定是直线！）
■ 成正比（形式ÿ =aX）只有当最佳拟合线是一条直线，通过原点（0,0）时才是成正比。
■ 多于两个交点，需要确认两个变量之间（例如X和ÿ）的关系。
■ 梯度：通过两点来确定，至少两点之间的距离是线的长度的一半：gradient = rise/run = ∆x/∆y
■ 梯度不确定度：
   ∆gradient = gradientMAX - gradientMIN/2
■ y截距的不确定度 ：                         
  ∆y - intercept = y - interceptMAX - y - interceptMIN/2

1.3 Vectors and Scalars

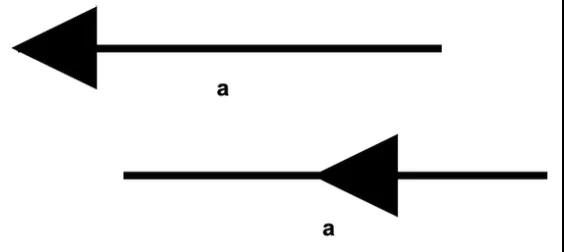
▲ Representation of a vector
向量是通过其端部或在其中间的箭头的线段表示，如以下两个相等的矢量：
■ 箭头指示方向。
■ 长度表示大小。

▲ Components of a vector
向量可以分解成一个垂直分量和一个水平分量，如下所示：

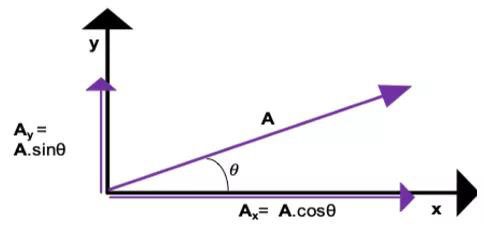
向量的梯度公式可以表示为：A ^ 2 = A X ^ 2 = A ý ^ 2。（即：毕达哥拉斯定理）
向量的方向（角度与水平）可以通过θ = tan^-1 Ay/Ax这个公式计算。
▲ Vector manipulation
当两个或多个向量相加或相减时，将形成合成向量。具体的计算参照下图：

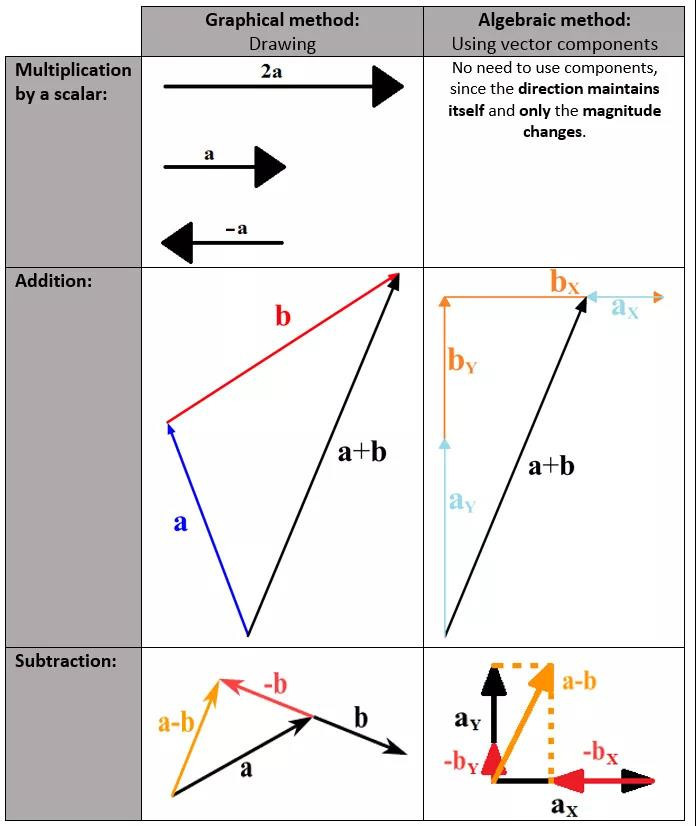
IB物理考纲 Topic1整理就分享到这里，希望能帮你夯实基础，稳扎稳打冲高分。

标化成绩是申请的基础，但IB过多的科目和论文要求、庞杂的知识点，又让很多同学焦虑不已。如果你对IB的多线作战感到乏力，点击预约试听【唯寻IB复习冲刺班】——

唯寻教学天团授课，

对考纲知识点进行重新切片，

全面提升归纳、审题、表达等学习力

帮学员养成学习惯性

还有TOK EE IA专项辅导修改，

考试技巧和国际课程基础两手抓，

帮你无限拉近与IB 40+的距离

唯寻学员的IB平均分高达40.19，远超亚太地区及全球IB平均分。

现在报名还能领取线上1V1测评，私人定制冲7方案哟。

更多IB学习攻略点击

2021年IB TOK论文放题，哪道最好拿A？唯寻解析来了

2021IB数学AI考纲新增了这些考点，教你如何针对性复习    

IB申请英国心理专业一般要考多高？什么样的选课更有利于申请    

【文末福利】

扫码添加小唯，

转发本文至朋友圈，

集齐10个赞，

她就会给你发50篇TOK SAMPLE大礼包

↑ Tutor小唯 你的专属留学顾问↑