
对于学习AP微积分的同学来说,级数是一个学习难点,不管是考试还是复习同学们都一定要认真点哦,下面我们给大家讲了一些AP微积分级数判断方法,希望大家能够记住这些判断方法。
几何级数判敛方法是七种方法中一个可以计算级数数值的方法,这也就意味着题目如果问级数计算的结果,那一定是用几何级数进行计算。而同时它明显的特征是前一项与后一项成比例。一旦判定了是几何级数,可以直接套用公式。
第n项判断只能判别发散,不能判别收敛,如果目标是快速判断发散,那nth term将是不错的选择。同时当你对某个级数一筹莫展的时候,不妨也用这个方法试上一试,它极有可能就是发散的。

积分法适用于把级数中的n改成x后一点儿也不违和的级数。积分法本质的原理就是利用函数积分,如果把n替换掉后的函数完全不认识,那就没有积分法的意义了。比如级数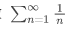 ,n换成x,就是
,n换成x,就是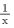 ,这是熟悉的幂函数。但是对于级数
,这是熟悉的幂函数。但是对于级数 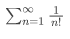 ,换为
,换为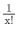 ,就很奇怪了,这并不是初等函数。
,就很奇怪了,这并不是初等函数。
P级数判别法是最迅速并且直接有效的级数判别手段,可以直接从给定级数的指数进行快速判断,比如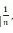 ,
,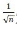 发散,
发散,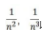 收敛。
收敛。

并且p级数可以结合有理函数的“找最大”的方法,可以将收敛与发散推广到更多的级数。比如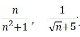 也同样发散,而
也同样发散,而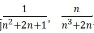 也同样收敛。
也同样收敛。
比较法是AP考试中比较冷门的方法,它最明显的特征就是,想要判敛必须有其他级数的辅助。比较的原理正是通过其他的级数特点进而推理待求级数的敛散性。
交替级数在众多判别方法中算是运算量比较大的一种,而且从逻辑上而言也并不简单,还需要一些记忆能力,掌握清楚具体应该怎么判断。但交替级数的优势也很明显,它有着典型的特点,只要级数的各项是在正负之间变化,那对应的方法都是交替级数判别法。
比值法,比值法对于奇形怪状的级数效果十分好,当进行约分时,很多奇怪的项数就会约分掉,极大的简化表达式。而且也是适用性最广的方法,即便是等比级数,也可以利用比值法进行检验,所以一旦觉得表达式整体诡异,那就用比值法,约掉之后,就会简单很多。级数判敛问题在第十章中占据一半的比重,而在我们的考试中,涉及到的判别方式只有这七种。
以下这些是给大家整理的一些泰勒级数公式:
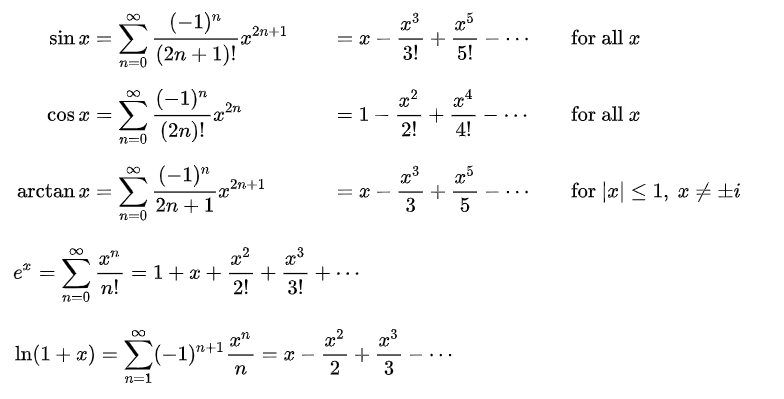
对于AP微积分复习我们也给大家带来了一些建议:
AP微积分AB建议从3月开始复习,直到5月上旬参加AP考试。3月份以学习并掌握微积分AB的相关知识点为主,4月份进入做题阶段。
AP微积分BC建议从2月份开始复习,直到5月上旬参加AP考试。2-3月学习并掌握微积分BC的相关知识点,4月份进入做题阶段。
AP微积分考试的重点在极限、导数以及积分的公式,其次对于报考AP微积分BC的同学需要专门用一定的时间学习级数,这是AP微积分中最难的内容。AP微积分不同于中国国内的出题方式,非常重视微积分的应用,简答题中通常都有具体的场景。所以,在学习导数以及定积分的内容时,要非常注重如何应用导数以及积分的工具解决实际问题,如增长率、旋转体体积、加速度-速度-位移、速率-总量的问题等。点击【预约试听】即可了解更多。

点击
查看更多。

学习有方法,成长看得见
筑梦牛剑/G5/常春藤
