在AP微积分中，定积分是属于第4章节，这部分经常会出现一些有关定积分应用的题型，下面就来给大家讲讲AP微积分定积分知识点吧。
黎曼和
使用近似逼近的方式来求面积，常用的是左端点、右端点、中点、梯形来做估计，步骤如下
(1）将区间等分成n份（也可不等分）
(2）按照预先设定的规则求出每一部分的面积
(3）加总。
利用黎曼和对定积分或面积进行估值，需要比较估计值和真实值的大小，可比较的是左端点、右端点和梯形三种估计方法，中点由于大小不易确定，较少出现。黎曼积分则是在加总之后求极限，那么该极限值应该等于图形面积的真实值，也就是定积分的值（黎曼可积）。
求定积分的基本方法
牛顿-莱布尼茨公式，使用该公式时先求不定积分，再代入数值，因此不定积分的方法都可以在这里使用。但是需要注意的是，使用换元法的时候，变量的取值范围会发生变化。
求定积分的特殊方法
对于某些规则图形（三角形、圆等）可用其几何意义直接算出面积，再利用定积分和面积之间的关系来求
利用奇函数和偶函数的性质来求。
积分中值定理
求函数在某一个区间上的平均值或积分中值，使用公式即可。
变限积分
当被积函数确定时，积分值会随着积分区间的变化而变化，因此可将积分值看做积分区间的函数，其中需要掌握的是变限积分的求导。
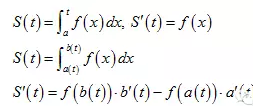
反常积分
当积分区间不是有限区间（即包含无穷大）或积分区间会使被积函数为无界的时候，求积分需要用到极限，如果极限存在，则称积分收敛（converge），不存在则称为发散（diverge）。
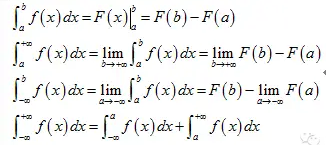
定积分的应用
面积
求平面曲线围成的平面图形的面积，一般来说是给定一条或若干条曲线，求它与x轴、y轴或其他直线或曲线围成图形的面积。
对于直角坐标系，使用定积分的几何意义来求，但需要注意的是面积永远是正数，而积分值有正有负，因此当函数大小关系或区间的边界发生变化时，要注意区别对待。
极坐标求面积
面积公式与直角坐标不同，特别需要注意的是积分的范围，如果不好判断，可用半径来反求角的范围。
体积：
求平行截面面积已知的立体图形的体积和旋转体体积，种图形对截面面积求积分可得体积，第二种图形有两种求法，种也是对截面面积求积分，不过要注意旋转截面是实心圆还是圆环，第二种是利用shell来求，掌握好展开后的圆柱壳的长宽高即可。
弧长
弧长公式用四种，一般来说在考试中如果是不允许使用计算器的部分，只会要求考生列出计算公式，不要求算出数值，而允许使用计算器的部分则可利用计算器来计算弧长的数值。
AP微积分BC考什么相关信息就分享到这里啦。AP微积分BC的复习是非常重要的，因为考试的答题节奏很紧张，如果复习阶段没有训练好考试状态，将面临会答题也来不及答的无奈，更不用说冲刺知名大学要求的满分了。今年AP还有1个月左右的复习时间，如果你想知道自己还存在哪些问题，可以点击预约试听【唯寻AP复习冲刺班】
点击
查看。
快扫码
关注老师微信
潘田翰(创始人)
剑桥大学化学工程硕士
Candise Cai
牛津大学化学硕士
Chris Chen
帝国理工学院物理学士
Ruby Rui
剑桥大学经济系学士&双硕士学位
Elaine Xu
牛津大学数学与统计专业学士
Olivia Hu
纽卡斯尔大学语言学专业硕士
Irene Liu
约翰霍普金斯大学国际关系/国际经济硕士
Mini Liu
东南密苏里州立大学双硕士
Shanshan Yu
英国伦敦政治经济学院金融学硕士
Stephy Tian
帝国理工化学硕士
Max Liu
帝国理工大学生物病毒学硕士
Sherry Lu
剑桥大学教育语言学硕士
Sue Pang
牛津大学经济与管理学士学位&LSE硕士
Jaryn Huang
牛津大学社会人类学专业哲学硕士
Peter Liu
牛津大学工程科学专业学士&硕士
Frances Zhu
牛津大学化学专业学士&硕士
Qianli Xia
剑桥大学数学系荣誉学士&硕士
Fang Yuan
美国普渡大学生物工程荣誉学士
Freda Yang
伦敦大学学院应用语言学硕士
Bo Su
范德堡大学英语教育硕士
Yuchen Yang
剑桥大学化学工程专业学士&硕士
Dora Liang
华威大学硕士
Tiffany Lin
伦敦大学学院经济学硕士
学习有方法，成长看得见
筑梦牛剑/G5/常春藤
唯寻导师推荐
换一换
Fang Yuan
美国普渡大学生物工程荣誉学士美国普渡大学生物工程荣誉学士
· 该生物工程专业连续多年US NEWS全美排名蝉联榜首
· 专攻微生物与细胞工程，在校期间参与微生物工程优化项目，并有BSL-2级别生物实验室工作经历
· 多年A-Level和AP辅导经验，成功帮助数百名学子圆梦美国名校
热门标签
唯寻导师访谈
沪ICP备18045704号-4 |
沪公网安备 31010502004453号
隐私安全
成功提交后我们将尽快与您联系，请注意来电哦！
微信咨询
成功提交后我们将尽快与您联系，请注意来电哦！
成功提交后我们将尽快与您联系，请注意来电哦！
