函数相关ALEVEL数学题目解析 带你看清关键考点解答步骤

函数是ALEVEL数学的必考知识点。本文就来分享一下有理函数相关的ALEVEL数学题目与解法，看答案解析前记得自己先尝试做一遍。

（点击查看数学不好可以申请英国大学吗？）

ALEVEL数学函数知识点考纲要求

以爱德思考试局为例，它要求同学们对函数考点做到：

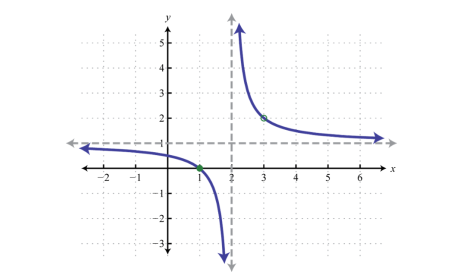
Functions to include simple cubic functions and the reciprocal functions y=k/x and y= k/x2 with x ≠ 0.  Knowledge of the term asymptote is expected.  

理解简单一元三次函数、反函数，并且理解渐近线的含义。

Students should be able to apply one of these transformations to any of the above functions (quadratics, cubics, reciprocals, sine, cosine, and tangent) and sketch the resulting graphs.   

考生应该能够将函数变换应用于任何一个函数（一元二次函数、三次函数、反函数、正弦、余弦和正切函数），并能勾画草图。

Given the graph of any function y = f(x), students should be able to sketch the graph resulting from one of these transformations. 

已知任意函数y=f(x)图像，学员能够画出经任何一种变换后产生的图像。

有理函数相关ALEVEL数学题目解析

1:∫xdx/(x+1)(x+2)(x+3)=∫[2/x+2-1/2/x+1-3/2/x+3]dx的详细过程!主要是分子是如何求得？

2.∫3/x^3+1=∫1/x+1+(-x)=2/x^2-x+1的详细过程!主要是分子是如何求得？

有理函数积分主要是部分分式的分解：

设Q(x)=c(x-a)^α...(x-b)^β(x^2+px+q)^λ...(x^2+rx+s)^μ

(其中p^2-4q<0,...,r^2-4s<0.).

那么真分式P(x)/Q(x)可以分解成如下部分分式之和：

P(x)/Q(x)=A1/(x-a)^α+A2/(x-a)^(α-1)+...+A[α]/(x-a)+...++B1/(x-b)^β+B2/(x-b)^(β-1)+...+B[β]/(x-b)+(M1x+N1)/(x^2+px+q)^λ+...+(M[λ]x+N[λ])/(x^2+px+q)+......+(R1x+S1)/(x^2+rx+s)^μ+...+(R[μ]x+S[μ])/(x^2+rx+s).

x/[(x+1)(x+2)(x+3)]=A/(x+1)+B/(x+2)+C/(x+3),

x=A(x+2)(x+3)+B(x+1)(x+3)+C(x+1)(x+2).

令x=-1,得A=-1/2,

令x=-2,得B=2,

令x=-3,得C=-3/2,

x/[(x+1)(x+2)(x+3)]=(-1/2)*1/(x+1)+2/(x+2)-(3/2)*1/(x+3),

或由x=(A+B+C)x^2+(5A+4B+3C)x+(6A+3B+2C),

比较系数得A+B+C=0,5A+4B+3C=1,6A+3B+2C=0,

得出A,B,C.

3/(x^3+1)=1/(x+1)(x^2-x+1)=A/(x+1)+(Mx+N)/(x^2-x+1),

3=A(x^2-x+1)+(Mx+N)(x+1).

令x=-1,得A=1,

(Mx+N)(x+1)=3-A(x^2-x+1)=-x^2+x-2=-(x-2)(x+1),

Mx+N=-x+2,M=-1,N=2.

3/(x^3+1)=1/(x+1)-(x-2)/(x^2-x+1).

有理函数相关ALEVEL数学题目解答就到这里。数学是大部分英国大学都很看重的选课，像计算机、会计、金融、工程等热门专业申请，没有数学成绩是不行的，而且想申知名大学，数学A*是肯定要拿到手的。

如果你想了解更多数学的学习技巧，或者提前适应新课的难度，可以点击预约试听【ALEVEL同步培训班】——

开设ALEVEL多项科目辅导

唯寻教学天团+助教+个人顾问多对一教学模式

针对不同考试局学员定制课程

预习、同步、冲刺等多种班型均有开设哟

更多ALEVEL学习攻略点击

alevel数学题目考什么内容？进阶数学 力学 统计数学复习攻略来了    

如何做好ALEVEL考前复习 牛剑大神是这样抓重点的