AP微积分中值定理公式分享会推导公式才能灵活应用哦-唯寻国际教育

在AP微积分中，中值定理是一个很高频的考点，尤其是罗尔中值定理和拉格朗日中值定理，很多人都感觉会傻傻分不清楚。那么下面我们就想来给大家有关AP微积分中值定理公式。

微分中值定理无论是在理论研究中还是在实际实践中都有这非常广泛的应用。

罗尔中值定理

罗尔中值定理是在费马引理的基础上做了一点引申，罗尔中值定理是，如果某个函数满足：在闭区间[a, b]上连续f(a) = f(b)在开区间(a, b)上可导那么，在区间(a, b)当中必然存在一个点X0，使得 AP微积分中值定理公式分享会推导公式才能灵活应用哦内容图片_1 。

这个中值定理也很容易想明白，既然函数在两个端点处值相等，那么无论它是先减再增还是先增再减或者是不增不减，那么显然都会存在至少一个极值点，既然存在极值点，那么根据费马引理显然就有导数为0的点。

拉格朗日中值定理

罗尔定理简单易懂，但是有一个小问题就是限制条件太死，函数上不一定能找到两个点相等。针对这个问题，拉格朗日对这个公式进行了拓展。他说，只要函数f(X0)满足：在闭区间[a, b]连续在开区间(a, b)可导那么就可以找到一个点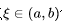 AP微积分中值定理公式分享会推导公式才能灵活应用哦内容图片_2 使得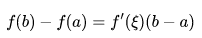：针对这个式子，我们做一个变形：

AP微积分中值定理公式分享会推导公式才能灵活应用哦内容图片_4

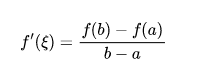
这个我们都非常熟悉，就是就是a和b两点连线的斜率。而则是函数在这点的切线，从几何角度上来看，说明存在一个点的切线和端点连线平行。

从定理上来看，如果a和b点的函数值相等，这个式子和罗尔定理完全一样，也就是说罗尔定理是拉格朗日中值定理的特殊情况。

柯西中值定理

柯西中值定理的图像和拉格朗日的一模一样，但是含义加深了一层。在我们之前的讨论当中，我们画的是y随着x变化的函数曲线。但是有可能X轴本身也是一个函数。也就是说之前我们画的是y=f(x)的图像，现在可能变成了的 AP微积分中值定理公式分享会推导公式才能灵活应用哦内容图片_5 图像，换句话说X轴和Y轴都是x的因变量，这里的小写的x成了一个参数。

在这样的函数当中，某一点的切线的斜率成了: AP微积分中值定理公式分享会推导公式才能灵活应用哦内容图片_6 。柯西中值定理正是作用于这样的函数上，如果函数f，F满足：在闭区间[a, b]上连续在开区间(a, b)上可导对于任意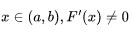，那么至少在(a, b)当中存在一点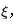满足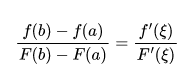

虽然这个公式看起来非常虎，但是证明方法和上面大同小异，我们引入一个基本上一样的辅助函数：

AP微积分中值定理公式分享会推导公式才能灵活应用哦内容图片_10

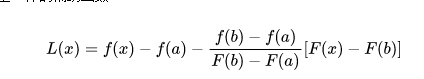
证明方法也是一样，可以发现这个辅助函数是满足罗尔定理的，那么我们对它求导，一模一样的方法就可以得到证明。

AP成绩已然成为进入美国优质大学的的敲门砖。对于申请哈佛、耶鲁、普林斯顿等优质知名大学的国际学校生来说，最好还是能向大学提供4-6门以上的AP成绩。而且只有理想分才会对申请才能起到比较大的作用。如果你觉得自己平时学得还行，但总离理想分差口气，点击报名【AP暑期先修班】，一线海归坐镇，适合所有校内与在校考生，8人小班能让每个学员的进度和需求受到关注，理想分自然更有助力。

AP微积分中值定理公式分享会推导公式才能灵活应用哦内容图片_11