马上就要到AMC竞赛的考试时间了，为例让大家更好的复习，掌握复习节奏，我们给大家整理了一些AMC10竞赛常考定理，这些地理常常在几何板块看到，下面就一起来看看吧！
平行线分线段成比例定理
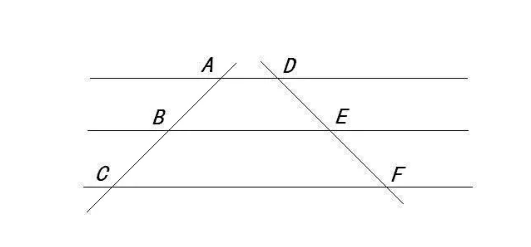
平行线分线段成比例定理指的是两条直线被一组平行线（不少于3条）所截，截得的对应线段的长度成比例。
推论：平行于三角形一边的直线，截其他两边（或两边延长线）所得的对应线段成比例。
方法
在利用平行线分线段成比例定理时,注意对应线段的位置.
由平行线+中点得线段中点,利用中位线解题.
定理推论：
平行于三角形一边的直线截其它两边（或两边的延长线）所得对应线段成比例。
平行于三角形一边，并且和其他两边相交的直线，所截得的三角形的三边与原三角形的三边对应成比例。
射影定理
射影定理，又称“欧几里德定理”：在直角三角形中，斜边上的高是两条直角边在斜边射影的比例中项，每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项。射影定理是数学图形计算的重要定理。
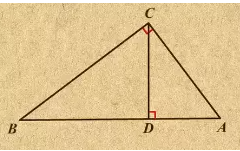
在Rt△ABC中，∠ABC=90°，BD是斜边AC上的高，则有射影定理如下：
BD²=AD·CD
AB²=AC·AD
BC²=CD·AC
角平分线定理
角平分线的定义：从一个角的顶点引出一条射线，把这个角分成两个完全相同的角，这条射线叫做这个角的角平分线。
从定义方面来理解：出现较角平分线，必然会出现相等大小的角，还会出现角之间的和、差、倍、分关系，在分析角平分线时需要注意向这方面去思考。
角平分线的性质：角平分线上的点到这个角的两边的距离相等。这是角平分线学习的重点，涉及角平分线的题目大都会运用到这个性质。
定理的作用
证明两条线段相等
用于几何作图问题
斯图尔特定理
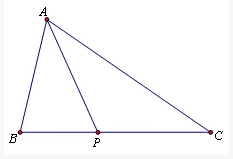
这个定理阐述了在一个任意三角形中由一点引出的到三角形对边的线段与其所分割的两条线段以及三角形三边的关系。如图二所示的一个三角形，从点A引出一条到边BC的线段交BC于点D，将BC分为线段m和线段n，如果三角形三边长为a，b，c，所作线段AD长为d，则有amn+ad^2=mb^2+nc^2，也可以记为man+dad=bmb+cnc。
以上就是关于AMC的干货分享了，如果您有参加竞赛需求的话，欢迎您点击在线咨询或者【预约报名】，唯寻能够满足您对于BBO、UKCHO、RES、USAD等国际竞赛方面的需求。
点击
AMC竞赛时间已提前3个月了 你需要这样一份AMC竞赛复习计划
澳洲AMC数学竞赛与美国AMC竞赛的区别在哪？这份全面对比表格都讲清楚了
查看。
换一换
沪公网安备 31010502004453号
成功提交后我们将尽快与您联系，请注意来电哦！
成功提交后我们将尽快与您联系，请注意来电哦！
