还有几个月就是AMC12的考试了，今天想来给同学们讲一讲有关AMC12复数考点信息，这个考点常常会和其他题型结合在一起。
复数的概念
虚数单位i
引入虎数单位i时，规定的两条性质：
①
②i可以与任何实数进行加法和乘法运算，且满足交换律、结合律，以及乘法对加法的分配律。
复数
把集合C={a+bi|a,b∈R}中的数，即形如a+bi(a,b∈R)的数叫做复数，其中i是虚数单位，全体复数所组成的集合C叫做复数集。
复数的代数形式
复数的代数形式z=a+bi(a,b∈R)，其中a与b分别叫做复数z的实部与虚部，它说明任何一个复数均可以由一个有序实数对确定。
复数的实部与虚部
对于复数a+bi(a,b∈R)，实部是a，虚部是b。
注意：在说复数a+bi时，一定有a，b∈R否则，不能说实部是a，虚部是b，复数的实部和虚部都是实数。
复数相等的条件
两复数相等的充要条件是两复数的实部和虚部分别对应相等，即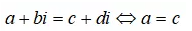
且b=d(a,b,c,d∈R)。
特别地，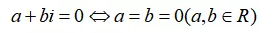
复数相等的充要条件是复数计算与解方程的依据，是把复数问题化为实数问题的最主要的方法，不能乱用复数相等的条件解题，另外，用复数相等的条件时要注意：
①化为复数的标准方式z=a+bi；
②实部、虚部中的字母为字数，即(a,b∈R)。
2、复数的几何意义
（1）任何一个复数z=a+bi(a,b∈R)用复平面内的点Z(a,b)，复平面内的点Z的坐标是(a,b)，而不是(a,bi)，也就是说，复平面内的纵坐标轴上的单位长度是1而不是i，由于i=0+1·i，所以用复平面内的点（0,1）表示i时，这点与原点的距离是1，等于纵轴上的单位长度，这就是说，当我们把纵轴上的点（0,1）标上虚数i时，不能以为这一点到原点的距离就是虚数单位i，或者i就是纵轴的单位长度。
（2）当a=0时，对任何b≠0，a+bi=0+bi=bi是纯虚数，但当a=b=0时，是实数，所以，除了原点外，纵轴上的点都表示纯虚数。
（3）复数z=a+bi(a,b∈R)中的z，书写时要小写；复平面内点Z(a,b)中的Z，书写时要大写。
AMC毕竟是地道的美式竞赛。中国学员还要面临语言能力、学术词汇能力、逻辑思维能力等附加门槛。如果想在不影响日常学习和申请的情况下高效复习，还是需要经验丰富的导师进行针对性和策略性的指导——点击报名【唯寻竞赛复习班】，知名大学海归一线竞赛导师授课，优选海量全真题库，高效梳理知识点与考试热点问题，全面启发竞赛思维。
点击
2021AMC12竞赛报名已开始 都说AMC12太难 来听选手说AMC12竞赛的难点在哪
查看。
换一换
沪公网安备 31010502004453号
成功提交后我们将尽快与您联系，请注意来电哦！
成功提交后我们将尽快与您联系，请注意来电哦！
