今年11月初的牛津大学MAT笔试,大家准备得怎么样呀?为了助力你的牛剑助力,唯寻笔试教研团队将先从函数Functions开始,配合牛津MAT真题,依次拆解重点难点,今天的文章就会从函数图像变化讲起吧。
MAT考试时间与含金量小科普
什么是牛津MAT数学考试?
MAT全称为Mathematics Admissions Test,是牛津大学测试本科(或本硕)数学、计算机相关专业考生的数学水平而举行的笔试。
此外申请帝国理工、华威大学的相关专业也需要通过这项考试。
牛津MAT真题考点解析
函数图像的变化 Transformations of a Function也是我们在⾼中阶段练习⽐较多的知识点,但是我们要学会区分函数和图像。函数永远是⼀个input对应⼀个output的,⽽图像,⽐如圆,就不⼀定是这样的 所以我们在理解图像的变化和函数变化时的思维也有所不同常见的函数变化有:
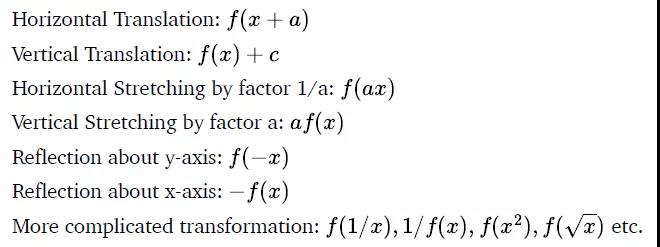
函数变化的顺序也很关键:
f(−x−2)可以理解为f(x)关于y轴对称得到f(−x)再向左平移2个单位f(−(x+2));也可以理解为f(x)向右平移2个单位f(x−2)再关于y轴对称得到f(−x−2),记住,FunctionTransformation要盯准x的变化。
⽽图像的变化较难概括,⽐如从x² + y² = 1到(x − a)² + (y− b)² = 1,或者是(x/a)² + (y/b)² = 1,虽然图像不难,但是和函数的transformations相⽐更难总结。

图片来自:网络
准确地说,图像本⾝是点的集合,Set of points. 判断图像以及图像的变化,我们需要锻炼的是对集合的直觉。
Siklos的AdvancedProblemsinMathematics这本书⾥的Problem14(也是STEP 1 1999年的⼀道题)就是很好的例⼦,有兴趣的同学可以去看他的解析,我们把思路精炼在这⾥:

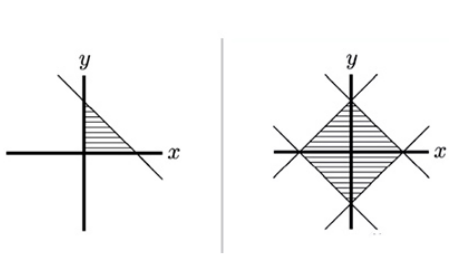
我们想知道 |x| + |y|⩽ 1在坐标系⾥的图像是怎样的,有同学看到绝对值就忍不住分情况讨论,这种autopilot的情况并不利于直觉的培养,绝对值函数很多时候蕴含着对称性,是可以利⽤的。
⾸先,我们把这个图像理解成点的集合,S= {(x, y) : |x| + |y|⩽ 1},那我们就不难发现,如果点(x, y) ∈ S则(−x, y), (x, −y), (−x, −y), (y, x)都在这个集合⾥,分别意味着图像关于y轴,x轴,原点,"y=x"对称。有了这个observation,我们就可以极⼤的简化我们的过程:
By symmetry, we can focus on the case where x,y ⩾ 0, so ...
⽤集合的思想去理解图像的变化,会⽅便我们理解更复杂的transformation,⽐如S₁={(x,y):|x−1|+|y−1|⩽1},so if (x,y)∈S₁ then (x−1,y−1)∈S, 所以我们把原图像向右向上各平移⼀个单位就可以得到了。
这样的题⽬在牛津MAT真题也出现过,⽐如2019年的第四题和2018年的第2题,这⾥我们⽤MAT2018Q2举例:

这道题⾥的Transformations S(x, y) 和 T (x, y) ⽤集合的思想去理解更为合适,尤其是最后⼀问,⽤集合的语⾔表⽰会清晰很多:
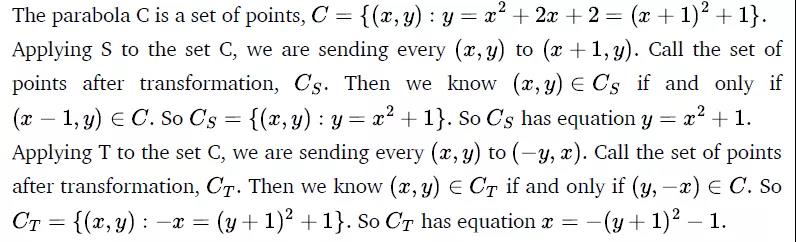
笔试本就是一场硬仗,在今年国际课程成绩普遍偏高的情况下,笔试考核更成为了学员展示学术能力和潜力的“第二战场”,也是牛剑发面邀,G5等其他院校发录取的重要依据之一。因此MAT、ECAA、ENGAA等笔试,大家都要脚踏实地来复习。有需要的话可以点击预约试听【唯寻牛剑笔试班】——
从大量真题中找出
常见考点、题型、出题方式
将复习计划分出轻重缓解
更有教学团队+助教+顾问多人把关学习进度
与你一同面对牛剑申请前哨站

更多牛剑笔试攻略点击↓











































 沪公网安备 31010502004453号
沪公网安备 31010502004453号





 成功提交后我们将尽快与您联系,请注意来电!
成功提交后我们将尽快与您联系,请注意来电!






 成功提交后我们将尽快与您联系,请注意来电!
成功提交后我们将尽快与您联系,请注意来电!


