牛津MAT考试复习资料分享 递归知识点答题技巧来啦

今年牛津MAT考试复习资料第三弹来啦，之前聊完了函数（点击查看），今天我们就讲讲第五大题经常会碰到的递归(Recurrence)。距离MAT11月3日开考还有十天左右，再坚持一下就会迎来胜利啦。

牛津MAT考试递归考点详解

很多学⽣在做MAT的时候会发现第五⼤题往往和递归有关系，是的，⼤家的感觉没错。

从出题⼈的⾓度考虑，第五⼤题涵盖了计算机和哲学的考点，重点就是数学的证明，递归思想和数学归纳的思想。

⽤Recursion的思想去解题⽬也是锻炼⼤家如何把复杂问题简化的过程，考验学⽣找相似点的能⼒。下⾯请看数学组导

师杨导师(Currently 哈佛博⼠后)对2019年第五⼤题的点评：

（点击这里预约试听他的课）

-解析时间-

2019年的第五道⼤题就是⼀个关于递归数列知识点的经典考题。在前两问的铺垫下，考官在第三问把重⼼转移到了构建数列上。

考官似乎是友善的：题⼲⾥不断凸显n+1，以及将两种情况以平⾏要点的形式列出，能看到考官明显的提⽰痕迹 。

事实上，MAT关于递归数列的考题经常会通过考虑两种情况来构建数列，这道题也算是⽼把戏了。

图片来自：牛津官网

题中，对于n+1这个特殊的元素来说，把它和其它元素当中的某⼀个划分到⼀起，意味着要把剩余的n−1个元素分配到k−1个集合⾥。否则便意味着，我们会先把n个元素分配到k个集合⾥，随后再把n+1放到某个集合当中。

因此：f(n+1,k)=nf(n−1,k−1)+kf(n,k)两种情况的背后蕴含的想法是，n+1这个元素所在的集合，要么仅仅包含两个元素，要么多于两个。

图片来自：网络

题⽬的指令看似平淡随和，事实上考官却期待着考⽣能够思路清晰地理清partition的概念，正确应⽤概率中的 “加法原理” 与 “乘法原理” ，甚⾄概率中 “条件期望” 这种⾼级⼯具。

这些想法对于⼤学学习数学分析，概率学以及随机过程都是必要的。由于⾼中阶段⽆法将这些概念讲透，考场上能够正确作答的考⽣，在某种程度上会⽐同龄⼈表现出更强的数学能⼒。这也是为何牛津MAT考试高分考⽣更容易受学校青睐的原因。

第三问的思路会直接影响到第四问的计算，考官决定要在这⾥拉开8分的巨⼤分差，展现了学校对于选拔高分者来录取的强烈倾向。

最后在第五问，题⽬询问了⼀个⾮常经典的问题。而这类的递归数列题⽬到最后，通常会有⼀个类似这⼀问的开放性问答，多种思路都可以得到正确答案。

严格遵循递归数列思路的同学，可以轻松的通过函数递归得出：

f(2n,n)=(2n−1)f(2n−1,n−1)=⋯=(2n−1)(2n−3)⋯3，进⽽通关整场考试。没能跟上考官进度的考⽣也有机会通过概率中的 “排列组合”弯道超车。
只是考试是公平的，前期有所⽋缺，⾃然会导致此时难度加⼤，若⾮有着极强的逻辑，⼤多数的概率处理都将是错误的。
如果将2n个元素排列，那么相邻的两个元素可以视为⼀组，正确答案需要考虑n组之间的排列，以及n组内的元素互换，即

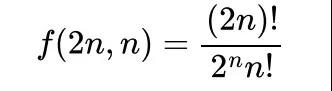
两个答案是相等的，牛津MAT考试的时候没必要纠结互相化简思路不同，答案展现形式⾃然不同。

-类举解析-

事实上很久以前剑桥三⼀学院就有过类似笔试题 “2n个⽹球运动员有多少种⽅法打⼀场初赛” 。

这和把2n个元素放进n个集合⾥是完全⼀致的，如果从2n个运动员中选取n个站在场地⼀端，另外n个可以通过排列选取对⼿。最后只要处理场地n组⽐赛场地两端的互换问题，即可得到同样的答案：

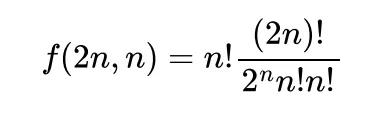
有时候递归数列的⼤题的结尾部分也可以⽤差分⽅程来处理。只是2019年的设定没有局限在线性差分⽅程当中，因此这样的思路不可取。有的考⽣处理题⽬经验丰富，⼼⾥对答案有所了解，那么数学归纳法在这种情况下也是个好的选择。
看完这篇递归考点详解，是否对MAT和唯寻的笔试教研团队有了更多的信心呢？笔试后面试也接踵而至，面试备战也已进入紧张期，抓紧时间准备起来吧，欢迎点击预约试听【唯寻牛津笔试 / 面试班】——

从大量真题中找出

常见考点、题型、出题方式

将复习计划分出轻重缓解

更有教学团队+助教+顾问多人把关学习进度

与你一同面对牛剑申请前哨站

更多牛剑申请攻略点击

牛津MAT考试考几分能被录取？申请牛津数学专业必读

牛津大学本科面试怎么应对？官方宣布了8大注意事项