欧几里得考点对数与指数讲解快来用这几道题试试手吧-唯寻国际教育

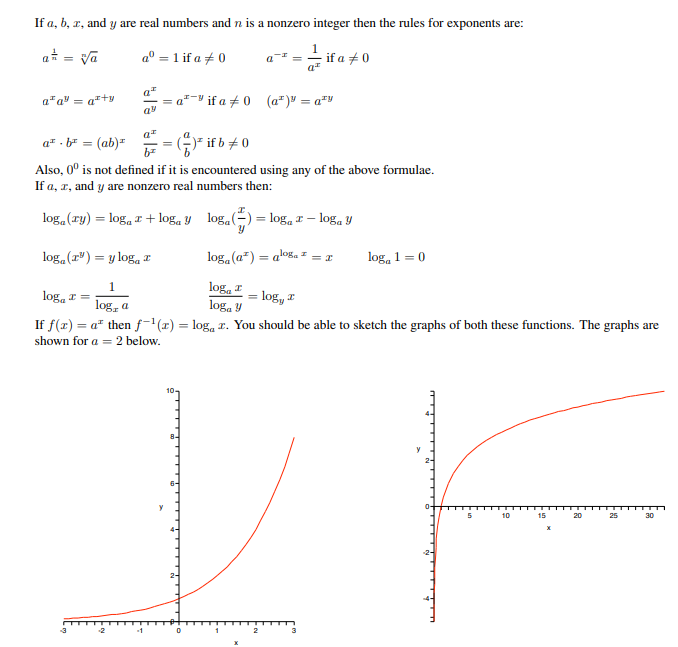
欧几里得竞赛考点涉及到众多内容，之前给同学们讲解了三角函数，本期就想来给大家讲讲欧几里得考点对数与指数，这部分其实要记住图像和一些基本的公式哦！

欧几里得对数与指数公式

欧几里得考点对数与指数讲解快来用这几道题试试手吧内容图片_1

Calculate the ratio x y if 2 log5 (x − 3y) = log5 (2x) + log5 (2y)

答案：First we note that if the 3 logarithmic terms are to be defined in the original equation then their arguments must be positive. So x > 0, y > 0, and x > 3y. Now 2 log5 (x − 3y) = log5 (2x) + log5 (2y) log5 (x − 3y) 2 = log5 (4xy). Now since the log function takes on each value its range only once, this implies (x − 3y) 2 = 4xy x 2 − 6xy + 9y 2 = 4xy x 2 − 10xy + 9y 2 = 0 (x − y)(x − 9y) = 0 So x y = 1 or 9. But x y > 3 from our restrictions so that x y = 9.

If m and k are integers, find all solutions to the equation 9(7k + 7k+2) = 5m+3 + 5m.

答案：We factor both sides of this equation to arrive at: 9(1 + 72 )7k = 5m(1 + 53 ) 3 2 · 2 · 5 2 · 7 k = 5m · 2 · 3 2 · 7 Now since both sides of this equation are integers and have unique factorizations it follows that m = 2 and k = 1 is the only solution.

Determine the points of intersection of the curves y = log10(x − 2) and y = 1 − log10(x + 1).

答案：Again the arguments of the log functions, x − 2 and x + 1 must be positive which implies that x > 2. Now CENTRE FOR EDUCATIONS IN MATHEMATICS COMPUTING 3 Euclid eWorkshop #1 LOGARITHMS AND EXPONENTS log10(x − 2) = 1 − log10(x + 1) log10(x − 2) + log10(x + 1) = 1 log10[(x − 2)(x + 1)] = 1 (x − 2)(x + 1) = 10 x 2 − x − 2 = 10 x 2 − x − 12 = 0 (x − 4)(x + 3) = 0 So x = 4 or −3, but x > 2 from our restrictions so x = 4. The point of intersection is (4, log10 2) or (4, 1 − log10 5). Since log10 2 + log10 5 = 1, these are equivalent answers.

看完了以上的这几题，下面这几题同学们都会不会做呢？

Determine x such that logx 2 + logx 4 + logx 8 = 1.
Determine the values of x such that 122x+1 = 23x+7 · 3 3x−4 .
What is the sum of the following series? log10 3 2 + log10 4 3 + log10 5 4 + · · · · · · log10 200 199 .
If x 3y 5 = 211 · 3 13 and x y 2 = 1 27 , solve for x and y.
If log8 3 = k then express log8 18 in terms of k.
Solve the equations for the point of intersection of the graphs of y = log2 (2x) and y = log4 x.
The points A(x1, y1) and B(x2, y2) lie on the graph of y = loga x. Through the midpoint of AB a horizontal line is drawn to cut the curve at C(x3, y3). Show that (x3) 2 = x1x2.
The function y = axr passes through the points (2, 1) and (32, 4). Calculate the value of r.
If 2 x+3 + 2x = 3y+2 − 3 y and x and y are integers, determine the values of x and y.
If f(x) = 24x−2 , calculate, in simplest form, f(x) · f(1 − x).
Find all values of x such that log5 (x − 2) + log5 (x − 6) = 2.
Prove that a, b, and c are 3 numbers that form a geometric sequence if and only if logx a, logx b and logx c form an arithmetic sequence.