对于一些想要申请数学专业的同学来说，参加一些高含金量的数学竞赛是非常有必要的，除了AMC以外，欧几里得也值得同学们来关注。下面就和大家分享一下欧几里得竞赛考点几何的知识点。
欧几里得数学竞赛是滑铁卢大学举办的几个数学竞赛之一，同时也是在这几个数学竞赛中对数学能力要求相对来说较高的一个。
考试范围有方程、方程组、不等式初等函数多项式函数（三次方程求根、余数定理和因式定理）指数函数和对数函数三角函数（图像、性质、正弦定理和余弦定理）数列和数列求和排列组合问题基础数论几何（平面几何、解析几何）
竞赛考点几何的知识点
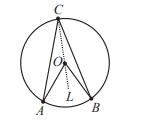
In the diagram we draw the line connecting C and O and let a point on CO extended be L. Since OA, OB and OC are radii we have that the triangles OAC and OBC are isosceles.
Thus ∠OAC = ∠OCA. Furthermore ∠OAC + ∠OCA = ∠AOL, the exterior angle of the triangle.
Therefore ∠OCA = 1/2 (∠AOL). Similarly ∠OCB = 1/2 (∠BOL). Adding these 2 results ∠ACB = ∠ACO + ∠OCB = 1/2 (∠AOL + ∠LOB) = 1/2 ∠AOB
练习题目
In a circle with centre O, two chords AC and BD intersect at P. Show that ∠AP B = 1/2 (∠AOB + ∠COD).
If the points A, B, C and D are any 4 points on a circle and P, Q, R and S are the midpoints of the arcs AB, BC, CD and DA respectively, show that P R is perpendicular to QS.
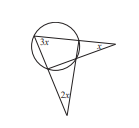
Calculate the value of x.
欧几里得竞赛考点几何的知识点就介绍到这里，如果你已经选好了比赛，还不知道如何复习，也可点击预约试听【唯寻竞赛复习班】，唯寻教学天团授课，覆盖多项主流国际竞赛，在助力解题速度与准确率的同时提升竞赛思维，让你轻松平衡课堂学习与竞赛复习，为知名大学录取奠定先发优势。
点击
查看。
换一换
沪公网安备 31010502004453号
成功提交后我们将尽快与您联系，请注意来电哦！
成功提交后我们将尽快与您联系，请注意来电哦！
