马上就要迎来了Alevel数学考试了，之前给大家讲解了一些微积分的难点和真题【Alevel微积分学习内容讲解？想学好微积分部分这6part的重难点你清楚吗？】、【爱德思Alevel微积分真题解析来啦！从真题角度总结答题规律拿A更简单】，今天给大家讲的是关于Alevel进阶数学的考试题型和考点，下面一起来看看Alevel数学FP1题型考点都有哪些吧！
二次函数和代数的混合求解计算
例：3x2 – 5x + 1 = 0，已经知道这个方程两个根分别是α和β，求解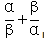
的结果。
对于一般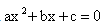
二次方程来说，除了传统的求根方式，还有一种解一元二次方程的途径，也就是
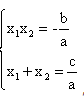，我们也把这种方法叫做韦达定理。那么通过
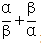把这个式子化简形成两可以用
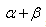来表示的形式，直接把二次函数对应的系数代入代数式求解即可。
归纳法证明题
归纳法证明题也是我们经常考题出现的形式之一，这种题的思路，就是对于第一项，要满足我们的适用性公式。其次假设第n=k项也满足公式，在假设的情况下，第k+1项按照正常的方式表达，并且可以整理成普遍适用性的形式，即可以证明结论对所有的positive number都成立。
例：
Prove by induction that for all positive integers n，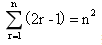
按照该题思路，首先证明n=1，LHS=
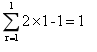RHS=1^2=1，由于LHS=RHS，所以the summation formula is true for n=1.
假设这个summation formula is true for n=k，
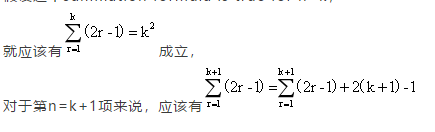
对上述式子整理得如下：
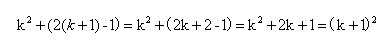
所以上述式子对于n=k+1也是适用，如果summation formula对于n=k成立，那么对于n=k+1也应该成立，n=1的时候该式也成立，那么现在可以证明对于所有的正整数，这个公式都适用。注意结论也很重要，不要忘记写。
矩阵的乘法运算求determinant
这应该也是FP1最简单的题型之一了，通常矩阵都是2x2的形式，在计算新矩阵的过程中，只需对应行和对应列相乘，这个时候一定不要看错行和列。
Complex numbers（复数）：复数的计算、共轭复数、复数的角和模长、方程的复数解
（Numerical methods）数值近似法：二分法，比例插值法，牛顿-拉普森方法
(Coordinate systems)曲线方程：参数方程曲线，抛物线的参数方程，双曲线的参数方程
（Matrix）矩阵：矩阵的计算，矩阵乘法，矩阵的行列式，反矩阵
（Series）数列求和：二次方和三次方的连续数列求和
（Induction）递推证明法：数列求和证明、整除性证明、递推公式证明、矩阵证明
这次的大考对冲刺牛剑G5的同学来说非常重要，因为不仅可以给申请省时间，还可以争取比你的竞争对手多考一门成绩。
如果你想用这次考试弥补上轮大考实力的遗憾、
如果还没有找到合适的复习方法，
如果有某门科目复习乏力，
点击报名【ALEVEL同步培训班】，
唯寻的导师95%毕业于海内外知名学府，
一对一同步辅导和先修和班课让
80%的学员单科复习1个等级以上
由班主任导师，国际课程导师，顾问导师和规划导师组成的
4人护航计划，更能助力复习效果
以下是唯寻在2019-2020年申请中拿到牛剑的表单，如果你的梦想也是牛剑，千万不要错过唯寻。
快扫码
关注老师微信
潘田翰(创始人)
剑桥大学化学工程硕士
Candise Cai
牛津大学化学硕士
Chris Chen
帝国理工学院物理学士
Ruby Rui
剑桥大学经济系学士&双硕士学位
Elaine Xu
牛津大学数学与统计专业学士
Olivia Hu
纽卡斯尔大学语言学专业硕士
Irene Liu
约翰霍普金斯大学国际关系/国际经济硕士
Mini Liu
东南密苏里州立大学双硕士
Shanshan Yu
英国伦敦政治经济学院金融学硕士
Stephy Tian
帝国理工化学硕士
Max Liu
帝国理工大学生物病毒学硕士
Sherry Lu
剑桥大学教育语言学硕士
Sue Pang
牛津大学经济与管理学士学位&LSE硕士
Jaryn Huang
牛津大学社会人类学专业哲学硕士
Peter Liu
牛津大学工程科学专业学士&硕士
Frances Zhu
牛津大学化学专业学士&硕士
Qianli Xia
剑桥大学数学系荣誉学士&硕士
Fang Yuan
美国普渡大学生物工程荣誉学士
Freda Yang
伦敦大学学院应用语言学硕士
Bo Su
范德堡大学英语教育硕士
Yuchen Yang
剑桥大学化学工程专业学士&硕士
Dora Liang
华威大学硕士
Tiffany Lin
伦敦大学学院经济学硕士
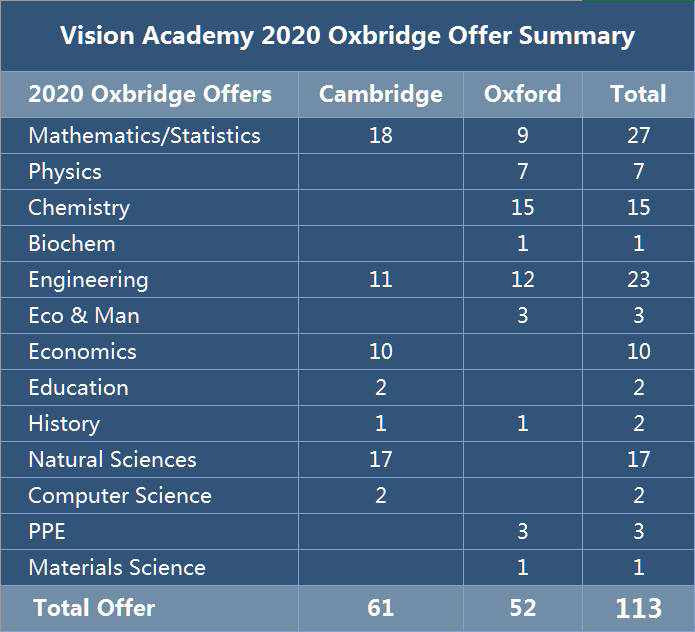
学习有方法，成长看得见
筑梦牛剑/G5/常春藤
唯寻导师推荐
换一换
Peter Liu
牛津大学工程科学专业学士&硕士牛津大学工程科学系荣誉硕士
· 以4A*的优异成绩申请进入牛津大学
· 前快消巨头全球管理培训生，曾任职于四大会计师事务所，前新媒体运营公司合伙人，前知名教育机构IGCSE/A-Level项目负责人
· 资深考试运动运动员，陪练员，教练员
· 擅长理工且兼修人文的知识爱好者及分享者
热门标签
唯寻导师访谈
沪ICP备18045704号-4 |
沪公网安备 31010502004453号
隐私安全
成功提交后我们将尽快与您联系，请注意来电哦！
微信咨询
成功提交后我们将尽快与您联系，请注意来电哦！
成功提交后我们将尽快与您联系，请注意来电哦！
