那些AP微积分常用公式汇总来了 看完这些记不住也会让你学会推导

选修AP微积分的同学是不是经常发现自己在考试中有时候会忘记公式，而导致失分。AP微积分公式那么多，同学们想要考出好成绩就一定要背熟、会推导。下面给大家汇总了一些AP微积分常用公式，一起来看看这些公式怎么推导吧！

AP微积分常用公式

会背、必须背熟

推导公式

换元法

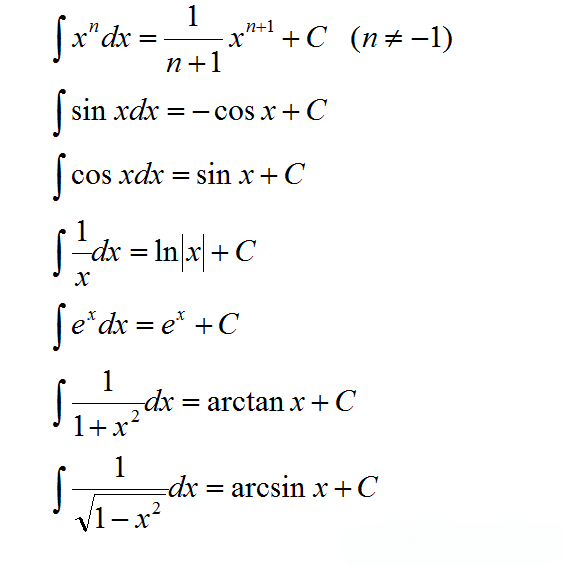
以下面这个为例，同学们知道这题该怎么换元吗？

解析:

凑微分法

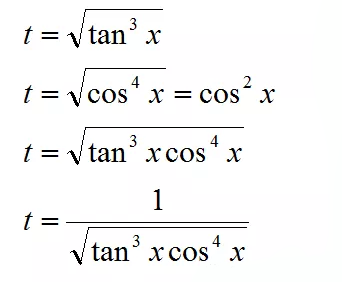
如果你看到积分式子中有这样的形式可以去凑，并且，剩余的部分只和右边括号里面的式子有关系，那么就可以用这样凑微分的方法来计算。

还是以这个为例

多项式分式

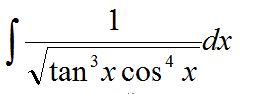
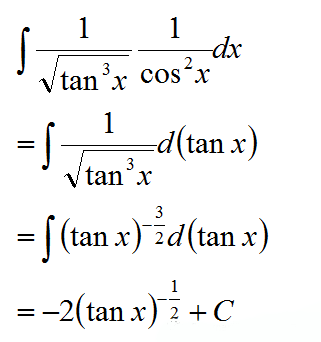
如果分母相对来说比较简单

比如这样的一些分母：

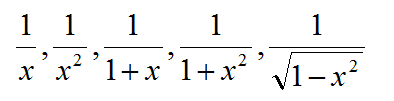
这些分母形式都是可以直接套用公式，或者通过简单的换元/凑系数的方法进行快速的积分，因此我们把他们归成简单的分母。

如果分子的最高次数大于等于分母的最高次数

比如

分子的最高次数都要大于等于分母的最高次数

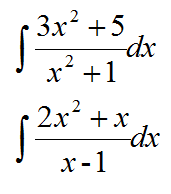
我们采取的方法是：拆分子

也就是把分子拆成多项来和分母约分，从而让最后的分式只保留分子较为简单的形式：

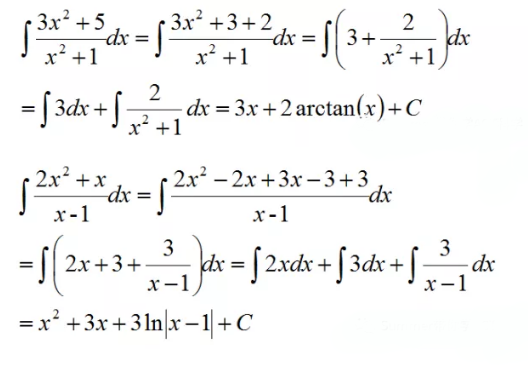
如果分母相对来说比较简单，但是分子的次数较小，这个时候我们需要对分母进行处理，如果分母出现是二次多项式的形式，我们可以把分母根据不同形式分成两种类型。

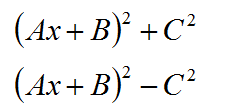
如果分母是种形式，我们把积分式子往arctan（x）的公式上去凑，比如：

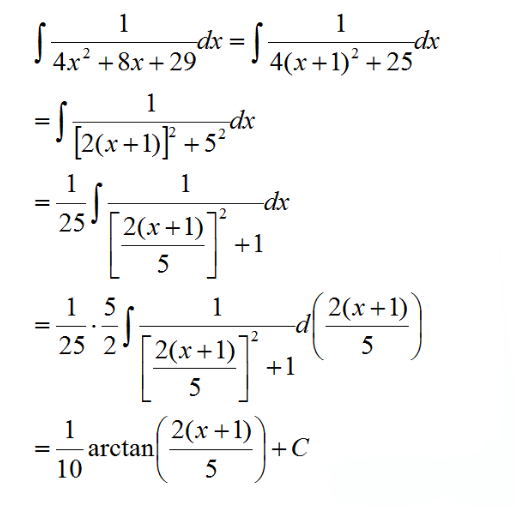
如果分母是第二种形式，我们需要进行因式分解，比如：

不管分子是简单的1，还是关于x的简单的低次多项式，都可以采取这个方法。

三角函数

三角函数中的做法比较多，不少题目都是涉及到凑微分的方法。比如我们看到下面几个形式：

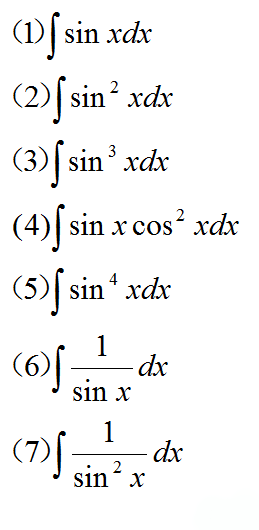
首先（1）比较简单，可以直接用公式计算。

（2），（5）这样的三角函数次数为偶次的，我们需要通过利用二倍角公式进行化简

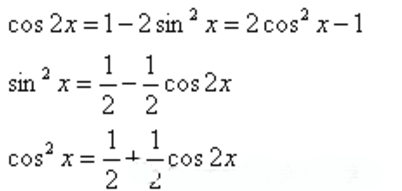
（3）（4）这样的如果三角函数的次数是奇次，我们需要把一个落单的三角函数拿出来凑微分

比如（3）：

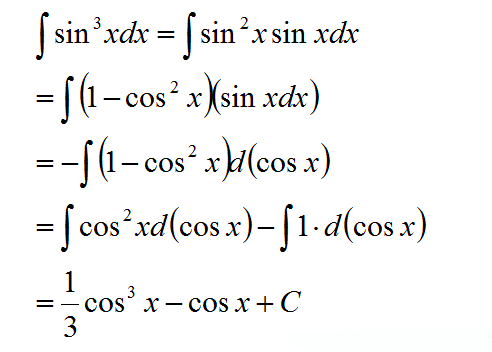
对于（6）这样的式子，因为sinx在分母上，我们不好凑微分，所以需要适当做出一些处理：

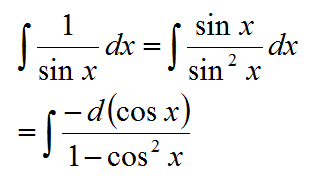
（7）这个式子：

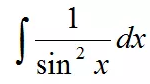
不要条件反射的想到偶次项用二倍角公式降次，请牢牢地记得这个公式：

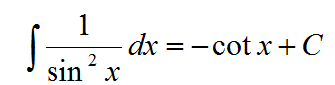
三角函数中还有一种特殊的换元

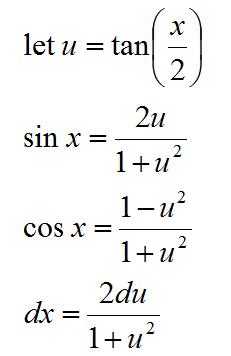
如果进行这样的换元以后，三角函数都可以被变换成多项式来处理。但是风险是：考试的时候可能选择题答案没有你算出来的答案。因为你的回答中一定会有tan(x/2)这样的形式，可能还需要进行三角变换才能得到选项中的答案。

带根号的式子

如果要积分的式子中有根号，一般我们有以下几种方法：

直接换元：直接把根号里面集体换元就好了。

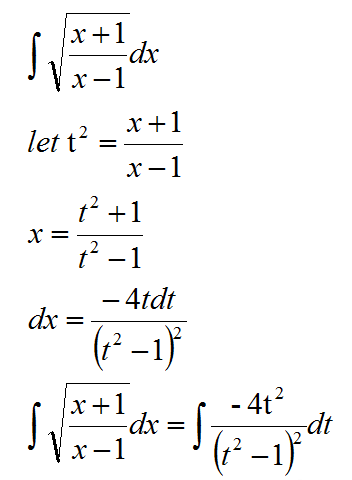
三角换元

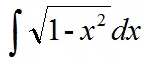
我们不能直接把整个根号换元，换元以后大家会发现又回到了这样的形式，所以这个时候我们需要通过三角函数来开根号：

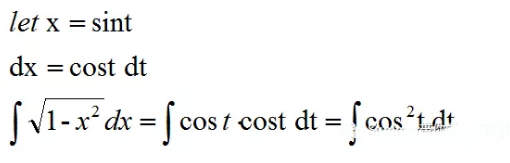
一般常用的换元式子：

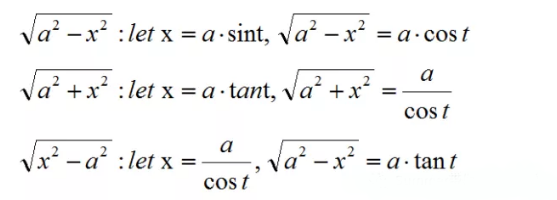
根号下内容相同，根号次数不同，选择最小公倍数

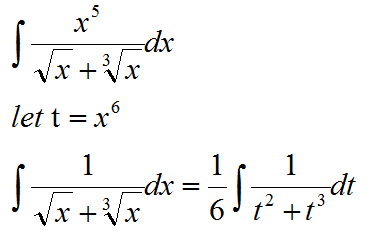
分母有理化，如果根号下内容不同，我们需要对分母进行简化：

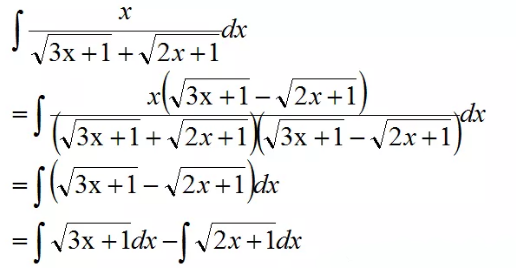
分部积分

分部积分主要运用于两种：两种不同形式乘在一起：

这时候我们利用分部积分的式子（求导乘法法则的变形）

u'和v的选择比较重要，一般情况下，我们对含有x的式子求导，对sinx，cosx和e^x进行积分。

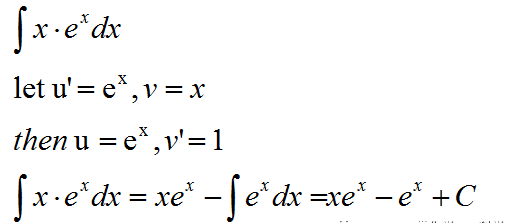
需要注意的是：如果需要通过两步分部积分计算的话，请保持两步中u'和v的选择形式一致。

无法计算积分的单独式子可以看成1乘以这个式子：

比如：

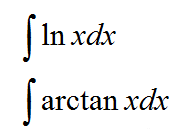
这两个式子，我们没有其他办法求积分，因此看成是1乘以这个式子：

今天对AP微积分理想分的公式解析就到这里，希望能帮助大家从一个新的角度理解考试的内容侧重。与ALEVEL不同，AP一年只能考一次，虽然可以二刷，但相同的科目考两遍必将严重影响复习效率，还会占据其他申请事项的准备时间，因此大家都要以一站上岸为目标啊。

如果你对明年大考的理想分还没有十足的信心，点击报名【AP全程班】——

唯寻教学天团精讲国际课程知识点

用充分的知识储备应对

AP灵活的考察体系

大部分课程结课都能无缝衔接大考

用最佳状态向满分发起冲击

点击

AP微积分AB和BC 这两门课程你会选择哪一个

2021年AP微积分会考什么 满分学长告诉你这7个必考点

查看。