今天的IGCSE数学知识点讲解给大家带来的就是向量了，对于以后有志于学数学的同学来说，向量是一个非常重要的地位，它不仅在应用数学中占据非常重要的作用，而且在现实生活中也应用的十分广泛。下面带大家一起来谈谈如何判定IGCSE数学向量方向吧！
首先，向量向量，顾名思义，向量是有2个部分组成的，向和量。向量不仅有自己的大小，同时还有一个方向。
一般用一个小箭头来表达向量，这个小箭头的长度是向量的大小，小箭头的方向就是这个向量的方向，我们可以把这个小箭头扔在直角坐标系当中，就像这样：
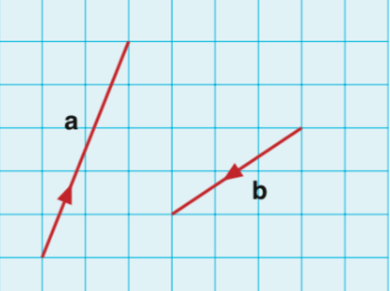
长度相同，方向相反，我们得到的是下面的向量：
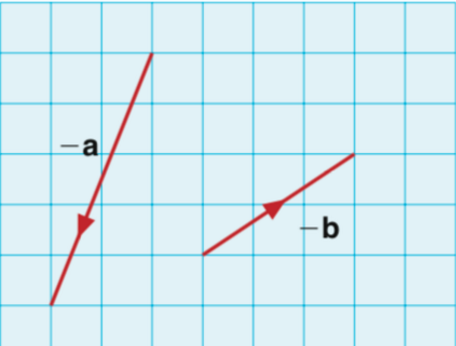
如果我们规定这些向量都是从原点出发的，我们可以将向量在直角坐标系中表示出来，箭头的小尖尖的横坐标和纵坐标就是这个向量的表达。于是我们现在就可以对向量进行加减啦！
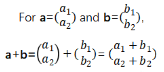
本质上，就是把两个向量的横坐标和纵坐标分别相加减。如果我们从物理中力的分解去理解这一知识点就非常的容易（正交分解），在这里我们不妨从图形的角度，看看究竟发生了什么。
将两个向量首尾相连，所谓的向量相加实际上就是各个向量叠加最终形成的一个结果，向量a的开头最终指向了b的结束点，这是最终的一个总体效果，所以从向量的相加来说无论我们将多少个向量进行相加，我们可以把这些向量首尾相连，从第一个起始向量的开端直接连接终止向量的末端的向量就是这些向量最终相加的结果。
因为向量是有方向的量，所以向量是有正负之分，在我们规定了正方向之后，与之相反的就是负方向，所谓负的向量就是与相应的正向量相比，大小相等，方向相反，由此我们就可以进行向量的减法，向量之间的减法本质上就是加上一个大小相等方向相反的向量，我们可以采用向量加法的思路来进行向量减法的计算。
那么我们可以用一个标量去乘以一个矢量吗？当然可以，本质上就是一个小箭头变成了一个大箭头，向量的方向不变，数量根据相应的放大因素作出改变，其结果当然也还是一个向量：
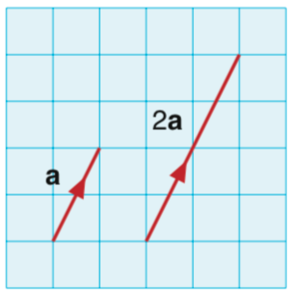
向量的方向往往非常直观，那么向量的大小我们该如何计算呢？向量的大小就是它箭头的长度，一个直角坐标系中的线段的长度我们该如何计算呢？我们一般会采用勾股定理来进行计算。
最后的最后，在向量中有一个概念非常非常重要，对于向量来说，方向相同且大小相同的向量就是同一个向量，这也是为什么一个向量可以在直角坐标系中进行移动，但是当我们讨论position vector的时候，我们箭头的出发点往往是以原点为出发点进行考量的，这时候就不能随心所欲的移动了。想明白这一点，对向量的学习非常重要。
大家现在对IGCSE数学了解了吗？想成功衔接到Alevel课程吗？那就赶紧来唯寻IGCSE课程班，带你将igcse知识点一网打尽。点击【预约试听】即可报名。
点击
IGCSE数学数列知识点讲解 P1和P2的公式大全都在这里了
IGCSE数学多项式函数题怎么解？这个方法能帮你快速找到解题捷径
查看。
快扫码
关注老师微信
潘田翰(创始人)
剑桥大学化学工程硕士
Candise Cai
牛津大学化学硕士
Chris Chen
帝国理工学院物理学士
Ruby Rui
剑桥大学经济系学士&双硕士学位
Elaine Xu
牛津大学数学与统计专业学士
Olivia Hu
纽卡斯尔大学语言学专业硕士
Irene Liu
约翰霍普金斯大学国际关系/国际经济硕士
Mini Liu
东南密苏里州立大学双硕士
Shanshan Yu
英国伦敦政治经济学院金融学硕士
Stephy Tian
帝国理工化学硕士
Max Liu
帝国理工大学生物病毒学硕士
Sherry Lu
剑桥大学教育语言学硕士
Sue Pang
牛津大学经济与管理学士学位&LSE硕士
Jaryn Huang
牛津大学社会人类学专业哲学硕士
Peter Liu
牛津大学工程科学专业学士&硕士
Frances Zhu
牛津大学化学专业学士&硕士
Qianli Xia
剑桥大学数学系荣誉学士&硕士
Fang Yuan
美国普渡大学生物工程荣誉学士
Freda Yang
伦敦大学学院应用语言学硕士
Bo Su
范德堡大学英语教育硕士
Yuchen Yang
剑桥大学化学工程专业学士&硕士
Dora Liang
华威大学硕士
Tiffany Lin
伦敦大学学院经济学硕士
学习有方法，成长看得见
筑梦牛剑/G5/常春藤
唯寻导师推荐
换一换
Frances Zhu
牛津大学化学专业学士&硕士牛津大学化学系荣誉学士&硕士
· Alevel取得A*A*AA的好成绩
· 大二期间就进入复旦大学先进材料实验室协助博士生进行纳米材料的课题研究
· 研究生期间利用Linux进行分子动力学模拟
· Frances老师开朗耐心，除了在学习成绩上给学生们提供帮助外，善于和学生成为朋友，敞开心扉的了解学生的内心，解决学生的心理障碍
热门标签
唯寻导师访谈
沪ICP备18045704号-4 |
沪公网安备 31010502004453号
隐私安全
成功提交后我们将尽快与您联系，请注意来电哦！
微信咨询
成功提交后我们将尽快与您联系，请注意来电哦！
成功提交后我们将尽快与您联系，请注意来电哦！
