AP微积分函数的知识点分享 赶紧来提前预习这门高含金量的科目吧

在AP微积分中函数有众多的几何特征，同学们都有了解过这些特征吗？下面来给大家讲讲AP微积分函数的知识点吧，希望大家都能够get到这里的知识点。 

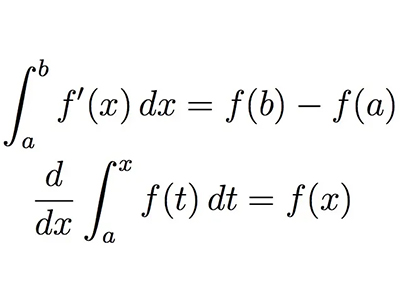
函数的几何特征：单调性、有界性、奇偶性、周期性、基本初等函数（幂函数、指数函数、对数函数、三角函数、反三角函数）表达式，定义域和图像，三角函数的恒等式的平方关系和倒数关系，三角函数的二倍角公式和半角公式，

三角函数的和差化积公式，正弦定理，余弦定理，复合函数，多项式函数，有理函数，极坐标和向量，解析几何中的抛物线方程，椭圆方程，双曲线方程，矩阵，数列，二项式定理，级数和极限等。我们这里就挑选一些给大家讲讲。

函数的定义域

（1）注意函数的自然定义域与实际定义域的区别与联系，对于有生成过程的函数，比如四则运算、复合运算所得函数，注意最终定义域的取值要助力运算过程的有效性。

（2）注意反函数的定义域、值域之间的联系，尤其注意与反函数相关问题的一个讨论过程中不要改变自变量、因变量的符号描述！除了最终的反函数描述！

函数的简单特性

(1) 有界性的讨论：定义法，注意无界与无穷大的区别与联系

(2) 单调性的判定：可导的情况下应用导数法，不可导的情况使用定义法

(3) 奇偶性的判定：定义法，注意函数为奇函数.

定义在区间内的任何函数都可以表示为一个偶函数与一个奇函数的和任何一个函数可以表示为两个非负函数的差

(4) 周期性的判定：定义法，注意周期与最小正周期的关系，并不是周期函数都有最小正周期。注意基本初等函数中三角函数的周期性，函数为周期函数，且为最小正周期．注意周期函数描述的曲线图形的“平移复制性”。

曲线的参数方程与极坐标方程

(1) 常见函数转换为参数方程描述的方法与参数方程消参数转换为显函数或方程描述的方法。注意参数方程的不性. 注意二元方程描述的方程转换为参数方程的常用方法，比如令y=tx转换参数方程.

(2) 极坐标方程与直角坐标方程、参数方程的互换。极坐标转换中注意点的位置与角度取值范围之间的关系.

数列极限存在性及计算的常规方法

一般数列极限的直接计算基于海涅定理（归结原则）转换为函数极限讨论.

(1) 常用数列极限的结论

(2) 数列极限的性质：性、有界性、保号性

(3) 数列极限的四则运算法则：一定注意极限存在并且分母极限不为零才能应用！即先判定再应用.

(4) 子数列与原函数的极限之间的关系：

子数列极限存在，原数列极限不一定存在，原数列极限存在，则子数列极限存在且相等，一个子数列极限不存在，或连个子数列极限虽然存在但是极限值不等，则原数列极限不存在。

函数极限的基本结论与性质

(1) 常见的函数极限结论：注意公式中的变量可以换成任意表达式，变量变化过程也可换成其他任意变化过程。

(2) 函数极限存在的基本性质：性、局部有界性、局部保号性.

函数的连续性与间断点

(1) 利用左右极限讨论函数的连续性：函数连续，则函数的左右极限都必须存在并且等于该点的函数值。

(2) 函数间断点的类型及其判定思路与方法

闭区间上连续函数的性质及其应用

(1) 看到闭区间上函数连续的条件，应该马上可以写出最值定理（有界性定理）、介值定理（零值定理）的结论。

(2) 会用零值定理证明根（函数的零点）的存在性。基本思路是：将等式移项，使其右侧等于0，将中值等式中的中值符号换成变量，令左侧表达式为函数，选择合适区间判定函数的连续性和端点值异号，基于零值定理验证中值的存在性，即方程根，或函数零点的存在性。

AP微积分理想分虽然高，但大部分AP学员都不会只参加一门考试。一般知名大学，需要提供4到6门左右的AP成绩。至于优质大学，每个同学提交的成绩至少在4门，并且要接近满分，无疑加大了AP的复习难度。如果你需要同时高效复习多门AP，但又不想耽误申请准备，可以点击预约试听【唯寻AP同步培训班】，唯寻教学天团授课，根据学员进度定制课程，从近年真题中解码考点，梳理高频知识点，帮助你效率冲刺分。

点击

AP微积分真题讲解 赶紧来收下这份最好的微积分复习资料吧

5个AP微积分复习小TIPS 让你拿理想分没商量

查看。