AP微积分BC真题解析，1道i题带你复习完6大考点

integral function是AP微积分BC里非常重要的工具，也是重点考试题型，一道integral function题目可能会同时考察学员的定积分几何意义、导数运用等多种能力，所以很有必要花时间集中攻克一下这类题。本文就结合一道AP微积分BC真题，和大家聊聊这类题的答题思路。

AP微积分BC考试介绍

AP微积分有两个科目，微积分AB和微积分BC。从学习内容上来看，BC基本涵盖了AB的内容，难度也更大。

通常来说，除非确定今后的专业方向是纯人文类专业，可以考虑选择微积分AB；

而对于社会科学、商科、管理类的学员，通常在大学里会需要完成两个学期以上的微积分课程，对于数学、计算机、工程、金融专业的学员更加是需要在此之后继续学习多元微积分的内容，因此推荐直接选择AP微积分BC。

而且，中国学员的数学能力普遍较强，所以大部分同学都会直接选择微积分BC。

AP微积分BC真题解析

题目：

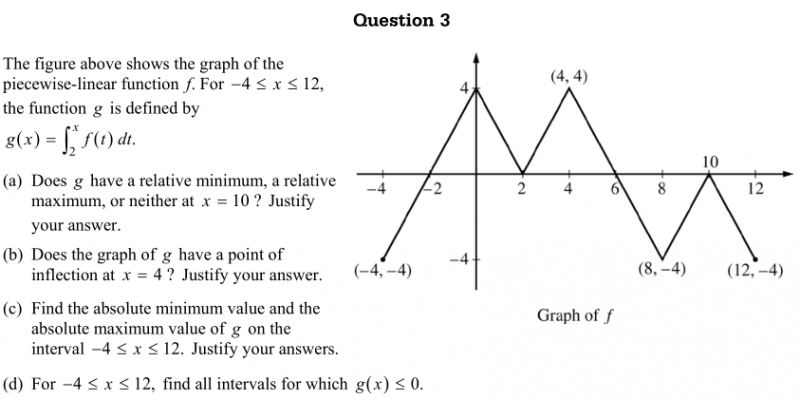
解析：

这道AP微积分BC真题考察了以下知识和重要结论

1. 积分函数的导数，定积分的基本运算

2. 导数的几何意义，导数等于0，和导数不存在的点的几何特征

3. Relative extrema 的判别

4. 闭区间上函数Absolute extrema 的计算

5. 二阶导数f’’(x)的意义

6. Point of inflection的判别

此外同学们还要熟悉关于定积分几个常见结论：

2.导数的几何意义，导数等于0，和导数不存在的点的几何特征

导数代表函数的切线斜率tangent line slope

直线的切线是它本身

常见结论：

f'(x)>0→ f(x) is increasing

f'(x)<0→  f(x) is decreasing

f'(x)=0→  f(x) has a horizontal tangent

f'(x)DNE →  f(x)has a cusp or a vertical tangent

3.Relative extrema 的判别

Step 1: 找到导数等于0和导数不存在的地方（critical point）

Step2：justify

A.f’(x) changes sign from positive to negative at x, then f(x) has a relative maximum at x

B.f’(x) changes sign from negative to positive at x, then f(x) has a relative minimum at x

C.f’(x) does not change sign at x, then f(x) has neither a relative maximum nor minimum at x

4.闭区间[a,b]上函数Absolute extrema 的计算

Step 1: 找到导数等于0与导数不存在的地方

Step2：列表计算f(a),f(x1),f(x2),f(b)比较大小（其中x1，x2分别指导数等于0，和导数不存在的地方）

5.二阶导数f’’(x)的意义

f’’(x)>0,f’(x) is increasing, f(x) is concave up

f’’(x)<0,f’(x) is decreasing, f(x) is concave down

6.Point of inflection的判别

Step 1: 找到二阶导数等于0和导数不存在的地方

Step2：justify

f’’(x) changes sign at x, f(x) has a point of inflection at x.

以上结论非常重要，同学们可以直接放在自己的错题集或者笔记里，对照以上6点，运用到实际解题场景中。

今日份AP微积分BC真题解析就到这里，希望能帮助大家更有针对性地复习。 

虽然CB刚刚确定了今年AP会采取线上+线下的考试方法，但CB已经明确公布CB将提供考纲一致、时长与题量也与线下完全一致的线上考试。所以不要抱有任何侥幸心理，扎扎实实把该学的都学了才是硬道理。

时间紧、任务重，如果你还不知道如何复习，点击预约试听【AP复习冲刺班】，唯寻教学天团授课，系统前测精准摸底，根据学员进度定制课程，从近年真题中解码考点，知识、方法与思维方式并重，帮你书写一份疫情下底气满满的标化成绩。

更多AP复习攻略点击

AP地理真题解析 改革后的人文地理这样复习才高效    

如何复习AP微积分AB/BC ？考点梳理带你走出公式地狱